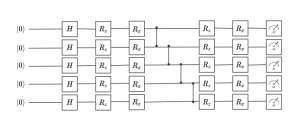
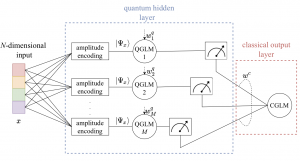
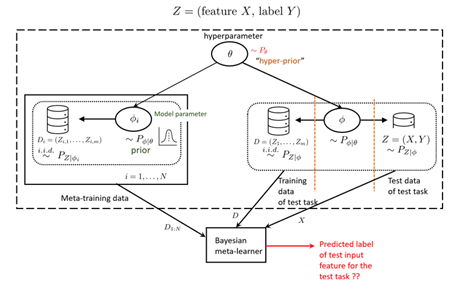
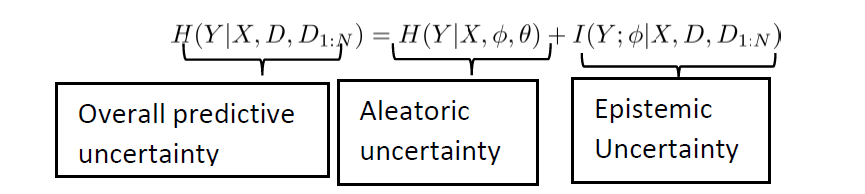
Motivation
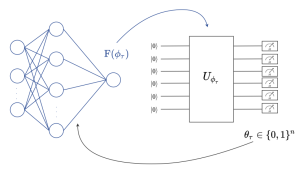
Artificial intelligence (AI) models typically report a confidence measure associated with each prediction, which reflects the model’s self evaluation of the accuracy of a decision. Notably, neural networks implement probabilistic predictors that produce a probability distribution across all possible values of the output variable. As an example, Fig. 1 illustrates the operation of a neural network-based demodulator, which outputs a probability distribution on the constellation points given the corresponding received baseband sample. The self-reported model confidence, however, may not be a reliable measure of the true, unknown, accuracy of the prediction, in which case we say that the AI model is poorly calibrated. Poor calibration may be a substantial problem when AI-based decisions are processed within a larger system such as a communication network.
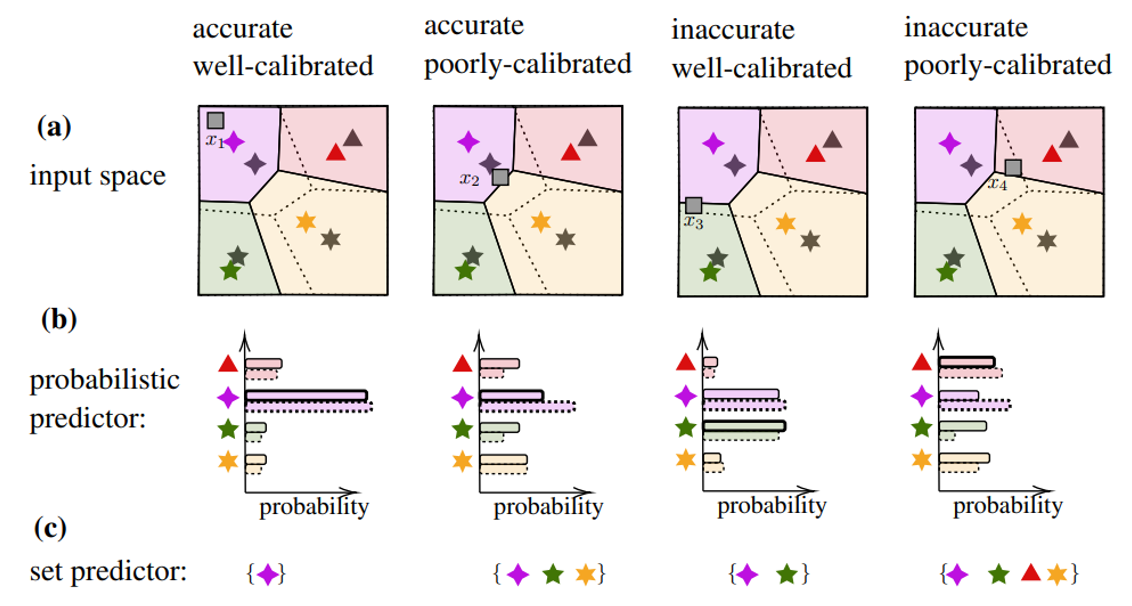
Fig. 1 Accuracy and calibration are different properties of probabilistic predictiors.
Set Predictors
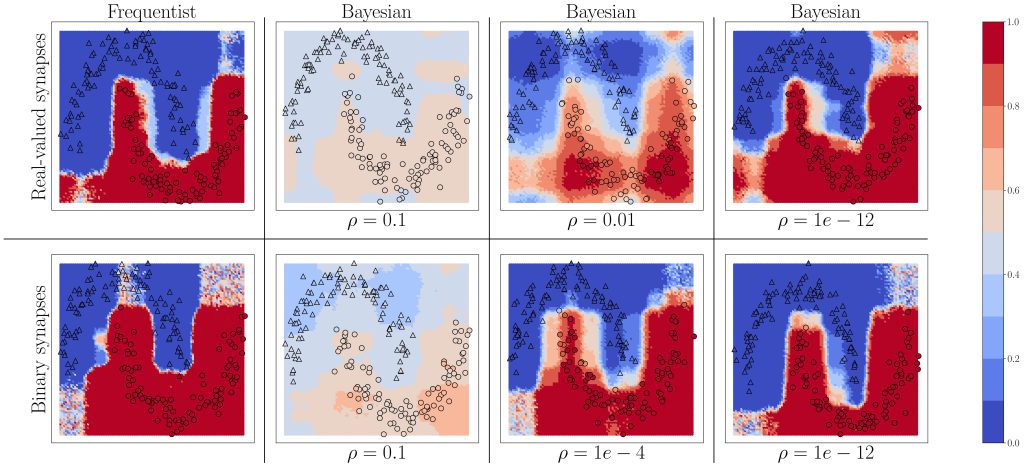
A set predictor is defined as a set-valued function that maps an input to a subset of the output domain based on a data set. As illustrated in the example of Fig. 1, it depends in general on an input, and can be taken as a measure of the uncertainty of the predictor. The performance of a set predictor is evaluated in terms of coverage and inefficiency. Coverage refers to the probability that the true label is included in the predicted set; while inefficiency refers to the average size of the predicted set. There is a clear a trade-off between two metrics.
Given a probabilistic predictor, one can construct a set predictor by relying on the confidence levels reported by the model. To this end, one can construct the smallest subset of the output domain that covers a fraction 1 − α of the probability designed by the trained model given an input. For poorly calibrated predictors, this approach cannot satisfy the coverage condition for the given desired miscoverage level α.
Conformal Prediction
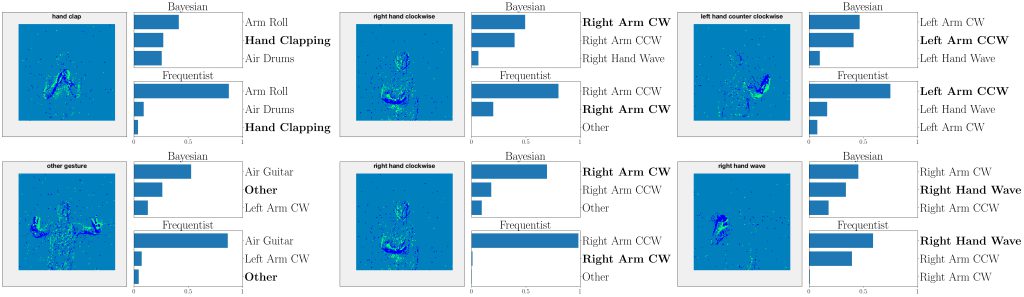
In our new work [3], presented at ICASSP2023, we applied three different conformal prediction schemes for a demodulation problem:
- Validation-based (VB) [1] – which partitions the available data set into training and validation sets. Uses the first set to train a model, and the second for calibration purpose.
- Cross-Validation-based (CV) [2] – which trains multiple models, each using all the available data set excluding one data point, that acts as a validation example. While increasing computational complexity, in general it reduces the inefficiency of the predictive sets.
- K-fold CV-based (K-CV) [2] – which cross-validates using a fold rather than a single point. K different models are trained using a leave-fold-out approach. This is a generalization of CV-CP set predictors that strike a balance between complexity and inefficiency by reducing the total number of model training phases to K.
Experiments
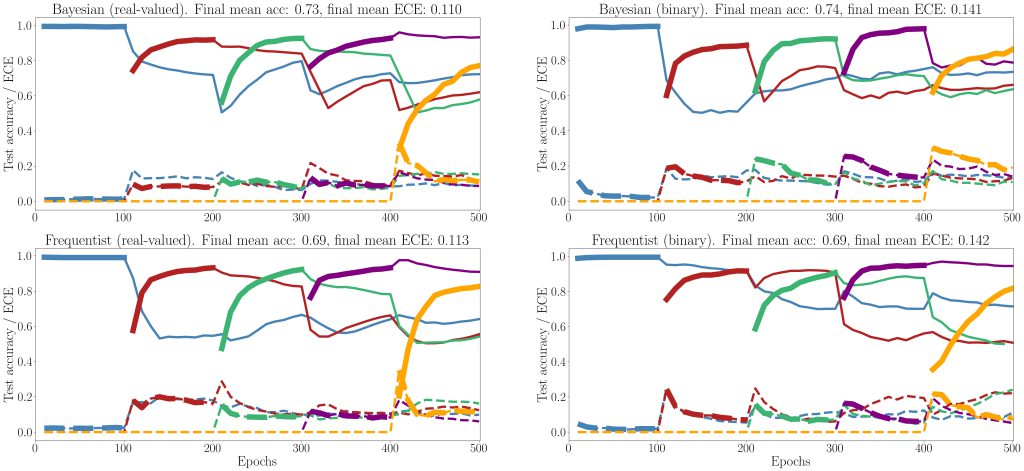
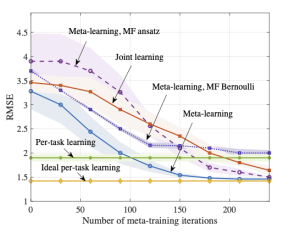
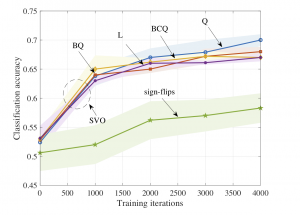
Fig. 2 shows the empirical coverage level and Fig. 3 shows the empirical inefficiency as a function of the size N of the available data set D. From Fig. 2, we first observe that the naïve set predictor, with both frequentist and Bayesian learning, does not meet the desired coverage level in the regime of a small number N of available samples. In contrast, all CP methods provide coverage guarantees, achieving coverage rates at least 1 − α. From Fig. 3, we observe that the size of the predicted sets, and hence the inefficiency, decreases as the data set size increases. Furthermore, due to their efficient use of the available data, CV and K-CV predictors have a lower inefficiency as compared to VB predictors. Finally, Bayesian NC scores are generally seen to yield set predictors with lower inefficiency, confirming the merits of Bayesian learning in terms of calibration.
Overall, the experiments confirm that all the CP-based predictors are all well-calibrated with small average set prediction size, unlike naïve set predictors that built directly on the self-reported confidence levels of conventional probabilistic predictors.
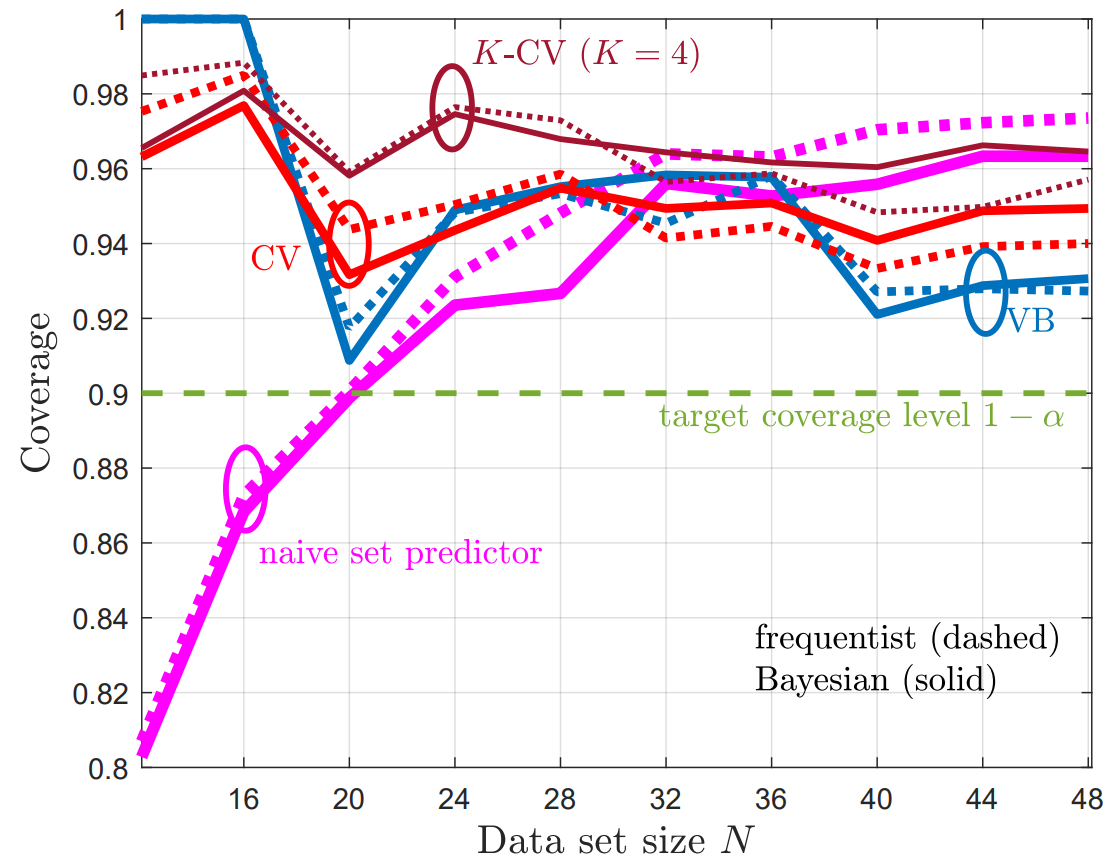
Fig. 2 Empirical coverage as function of data set size
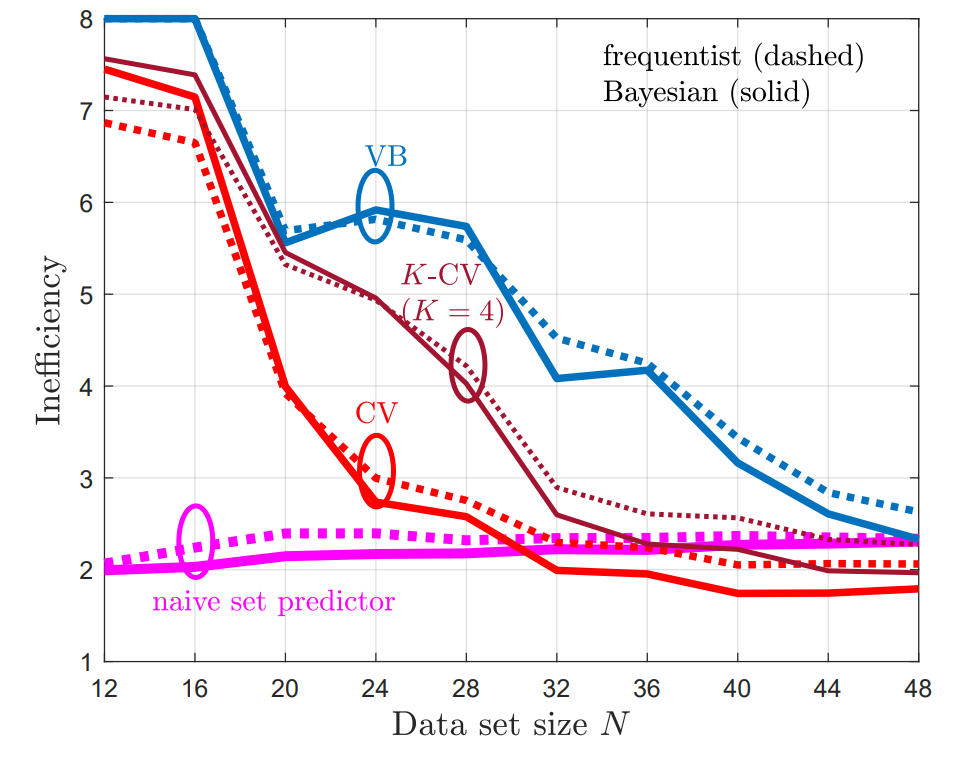
Fig. 3 Empirical inefficiency as function of data set size
Please see preprint of the ICASSP23 paper for full details.
[1] Vovk, Vladimir, Alexander Gammerman, and Glenn Shafer. “Algorithmic learning in a random world,” Vol. 29. New York: Springer, 2005.
[2] Barber, Rina Foygel, Emmanuel J. Candes, Aaditya Ramdas, and Ryan J. Tibshirani. “Predictive inference with the jackknife+.” (2021): 486-507.
[3] Cohen, Kfir M., Park, Sangwoo, Simeone, Osvlado, and Shamai, Shlomo (Shitz). “Calibrating AI Models for Wireless Communications via Conformal Prediction,” to appear in ICASSP 2023 [Online]. Available: https://arxiv.org/abs/2212.07775


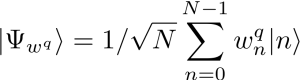
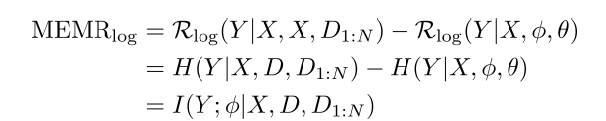
Recent Comments