Whilst the true impact of quantum computers is anybody’s guess, there seems to be some consensus on the advantages offered by near-term devices in modeling more complex probability distributions. These distributions can be used to model complex particle interactions, e.g., in quantum chemistry, or, as we will see next, to train principled machine learning models – in this case, binary Bayesian neural networks – and enable fast adaptation to new learning tasks from few training examples.
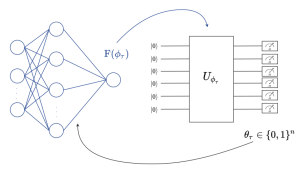
Fig. 1. (left) A binary Bayesian neural network, i.e., a neural network with stochastic binary weights, is trained to carry out a learning task. (right) The probability distribution of the binary weights of the neural network is modelled by a Born machine, i.e., by a parametric quantum circuit (PQC), leveraging the PQC’s capacity to model complex distributions [1].
Setting
In our latest work, accepted for presentation at the IEEE MLSP, we are interested in training Bayesian binary neural networks, i.e., classical neural networks with stochastic binary weights, in a sample-efficient manner by means of meta-learning, as illustrated in Fig. 1. The key idea of this work is to model the distribution of the binary weights ![]() via a Born machine, i.e., via a probabilistic parametric quantum circuit (PQC), due to the capacity of PQCs to efficiently implement complex probability distributions [1]-[4]. We propose a novel method that integrates meta-learning with the gradient-based optimization of quantum Born machines [3], with the aim of speeding up adaptation to new learning tasks from few examples.
via a Born machine, i.e., via a probabilistic parametric quantum circuit (PQC), due to the capacity of PQCs to efficiently implement complex probability distributions [1]-[4]. We propose a novel method that integrates meta-learning with the gradient-based optimization of quantum Born machines [3], with the aim of speeding up adaptation to new learning tasks from few examples.
Born Machines
A Born machine produces random binary strings ![]() , where
, where ![]() denotes the total number of model parameters, by measuring the output of a PQC
denotes the total number of model parameters, by measuring the output of a PQC ![]() defined by parameters
defined by parameters ![]() .
.
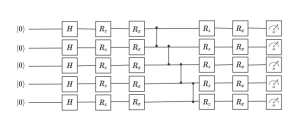
Fig. 2. Hardware-efficient ansatz for a Born machine. All qubits are initialized in the ground state. The rotations are parametrized by the entries of the variational vector.
As illustrated in Fig. 2, the PQC takes the initial state ![]() of n qubits as an input, and operates on it via a sequence of unitary gates described by a unitary matrix
of n qubits as an input, and operates on it via a sequence of unitary gates described by a unitary matrix ![]() . This operation outputs the final quantum state
. This operation outputs the final quantum state
![]()
which is measured in the computational basis to produce a random binary string ![]() . Note that each basis vector of the computational basis corresponds to one of all the possible 2^n patterns of model parameters
. Note that each basis vector of the computational basis corresponds to one of all the possible 2^n patterns of model parameters ![]() .
.
The PQC can be implemented using a hardware-efficient ansatz [2], in which a layer of one-qubit unitary gates, parametrized by vector ![]() , is followed by a layer of fixed, entangling, two-qubit gates. This pattern can be repeated any number of times, building a progressively deeper circuit. Another option is using the mean-field ansatz that does not use entangling gates, and only relies on one-qubit gates.
, is followed by a layer of fixed, entangling, two-qubit gates. This pattern can be repeated any number of times, building a progressively deeper circuit. Another option is using the mean-field ansatz that does not use entangling gates, and only relies on one-qubit gates.
By Born’s rule (hence the name of the circuit), the probability distribution of the output model parameter vector ![]() is given by
is given by
![]()
Importantly, Born machines only provide samples, while the actual distribution above can only be estimated by averaging multiple measurements of the PQC’s outputs. Therefore, Born machines model implicit distributions, and only define a stochastic procedure that directly generates samples.
Some Results
Fig. 3 illustrate the results in terms of the prediction root mean squared error (RMSE) as a function of the number of meta-training iterations. By comparison with conventional per-task learning, the figure illustrates the capacity of both joint learning and meta-learning to transfer knowledge from the meta-training to the meta-test task, with hardware-efficient (HE) and mean-field (MF) quantum meta-learning clearly outperforming joint learning. For example, HE meta-learning requires around 150 meta-training iterations to achieve the same RMSE ideal per-task training, whilst joint-learning requires more than 200 to achieve comparable performance. The HE ansatz performs best, due to the use of entangling unitaries; however, the MF ansatz approaches the minimal RMSE after 230 iterations. The classical solution based on MF Bernoulli does not achieve lower RMSE than the quantum-aided meta-learning schemes, even with joint learning.
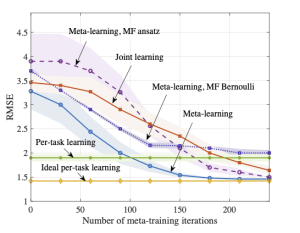
Fig. 3. Average RMSE for a new, meta-test, task as a function of the number of meta-training iterations. The results are averaged over 5 independent trials.
Please see the paper for a more detailed exposition, available here.
References
[1] Arute, F., Arya, K., Babbush, R., Bacon, D., Bardin, J.C., Barends, R., Biswas, R., Boixo, S., Brandao, F.G., Buell, D.A., et al.: Quantum supremacy using a programmable superconducting processor. Nature 574(7779), 505–510 (2019)
[2] Kandala, A., Mezzacapo, A., Temme, K., Takita, M., Brink, M., Chow, J.M., Gambetta, J.M.: Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549(7671), 242–246 (2017)
[3] Liu, J.G., Wang, L.: Differentiable learning of quantum circuit Born machines. Physical Review A 98(6), 062324 (2018)
[4] Sweke, R., Seifert, J.P., Hangleiter, D., Eisert, J.: On the quantum versus classical learnability of discrete distributions. Quantum 5, 417 (2021)

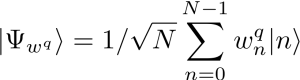
Recent Comments