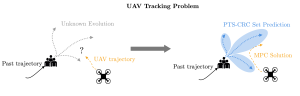
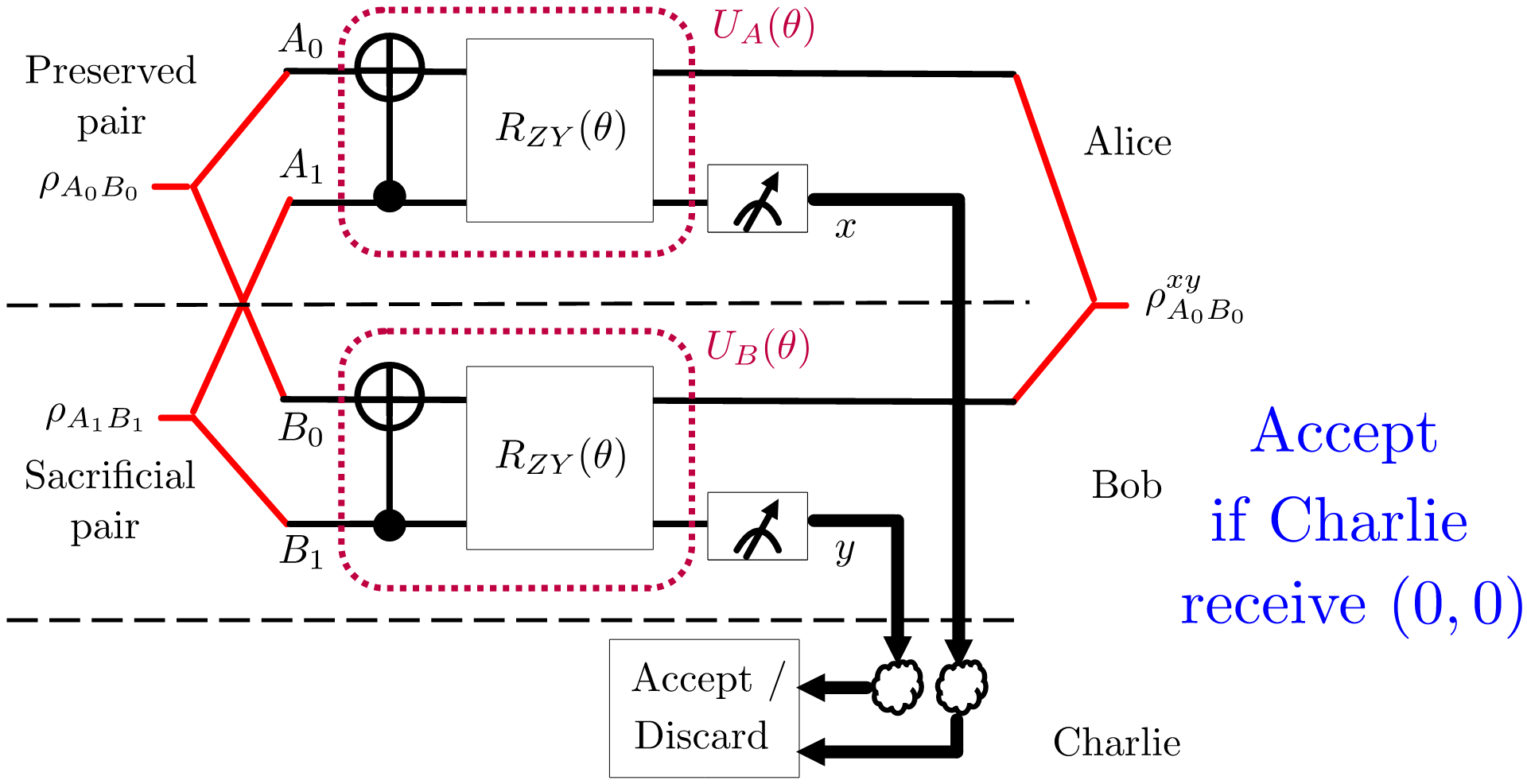
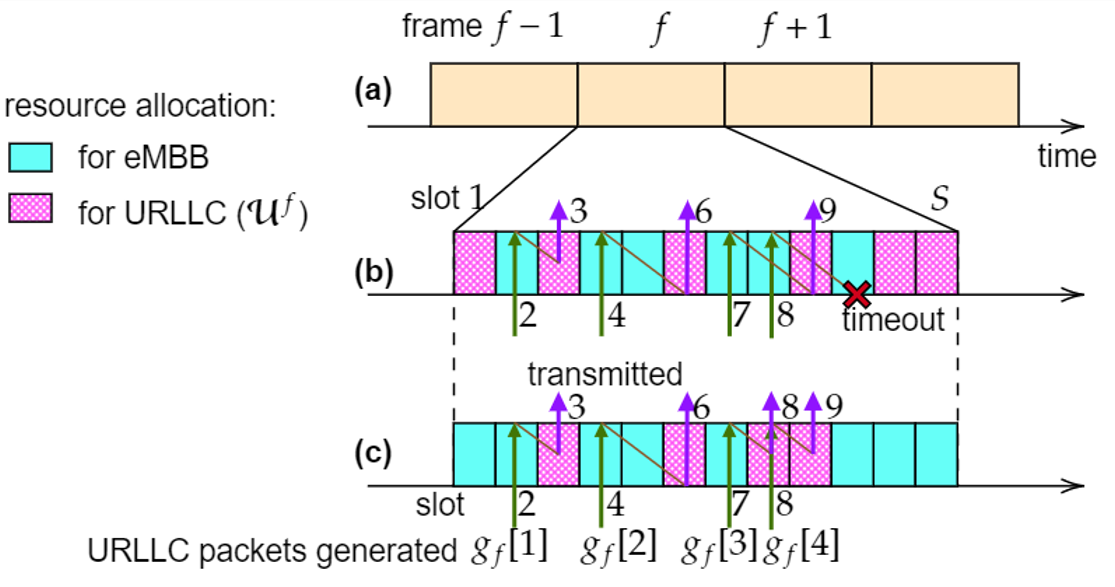
Motivation
In the general formulation of black-box optimization problems, a designer sequentially attempts candidate solutions, receiving noisy feedback on the value of each attempt from the system. As illustrated in Fig. 1, we consider scenarios in which feedback is also provided on the safety of the attempted solution, and the optimizer is constrained to limit the number of unsafe solutions that are tried throughout the optimization process [1] [2]. Focusing on methods based on Bayesian optimization (BO), prior works provide safety guarantee that any unsafe solution is excluded with a controllable probability with respect to feedback noise. This theoretical guarantee is, however, only valid if the optimizer has access to information about the constraint function, e.g., reproducible kernel Hilbert space (RKHS) norm bound of the constraint function. In practice, specifying such information may be difficult, since the constraint function is a priori unknown.
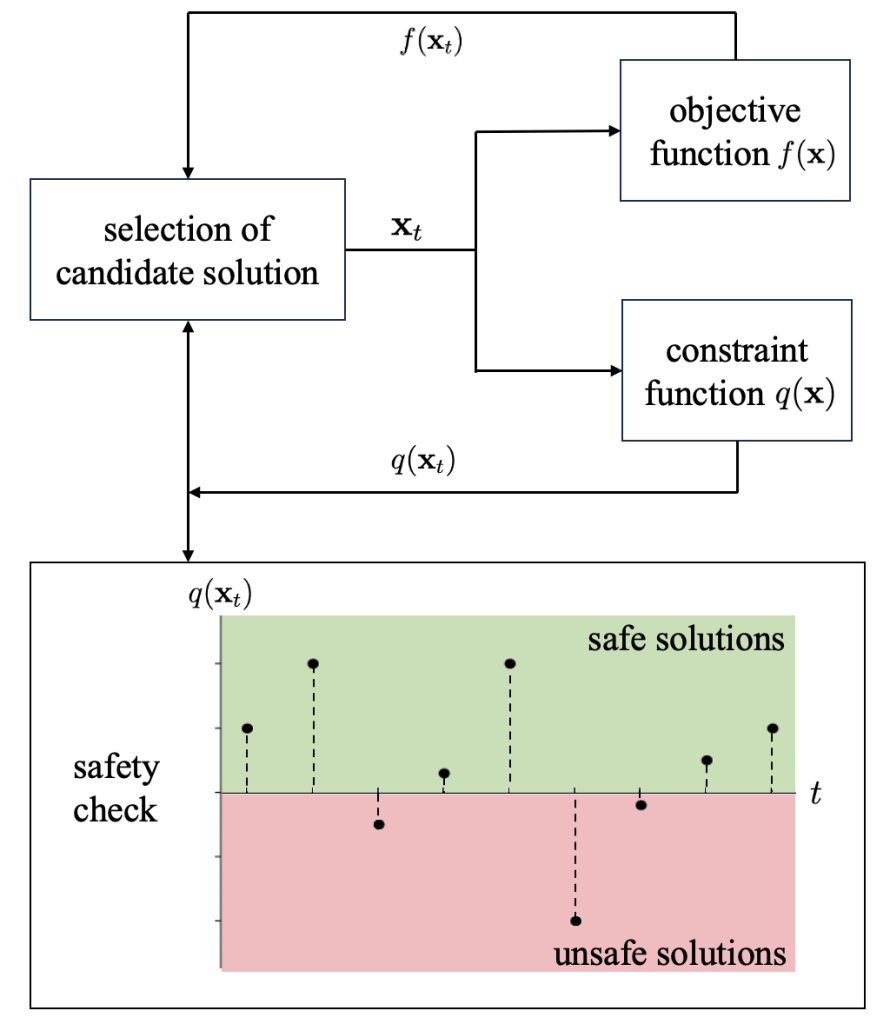
Fig. 1. Illustration of black-box optimization with safety constraints. We provide formal safety guarantee on keeping the fraction of unsafe solutions attempted during the optimization process below some tolerated threshold.
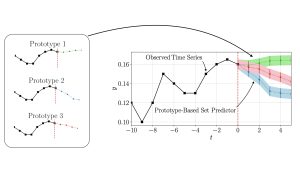
Safe-BO via Online Conformal Prediction
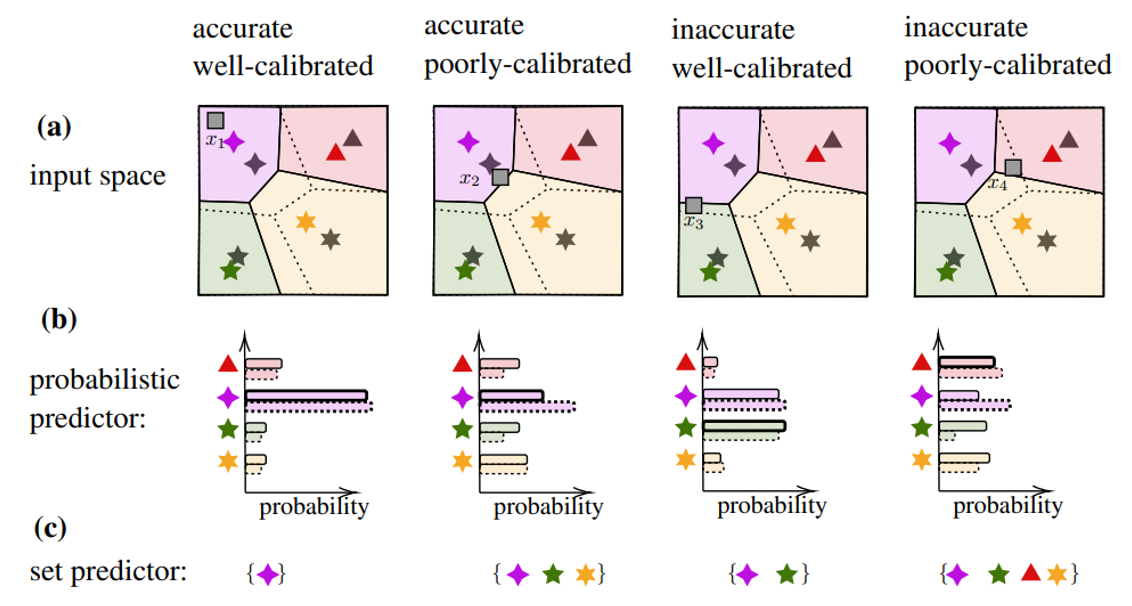
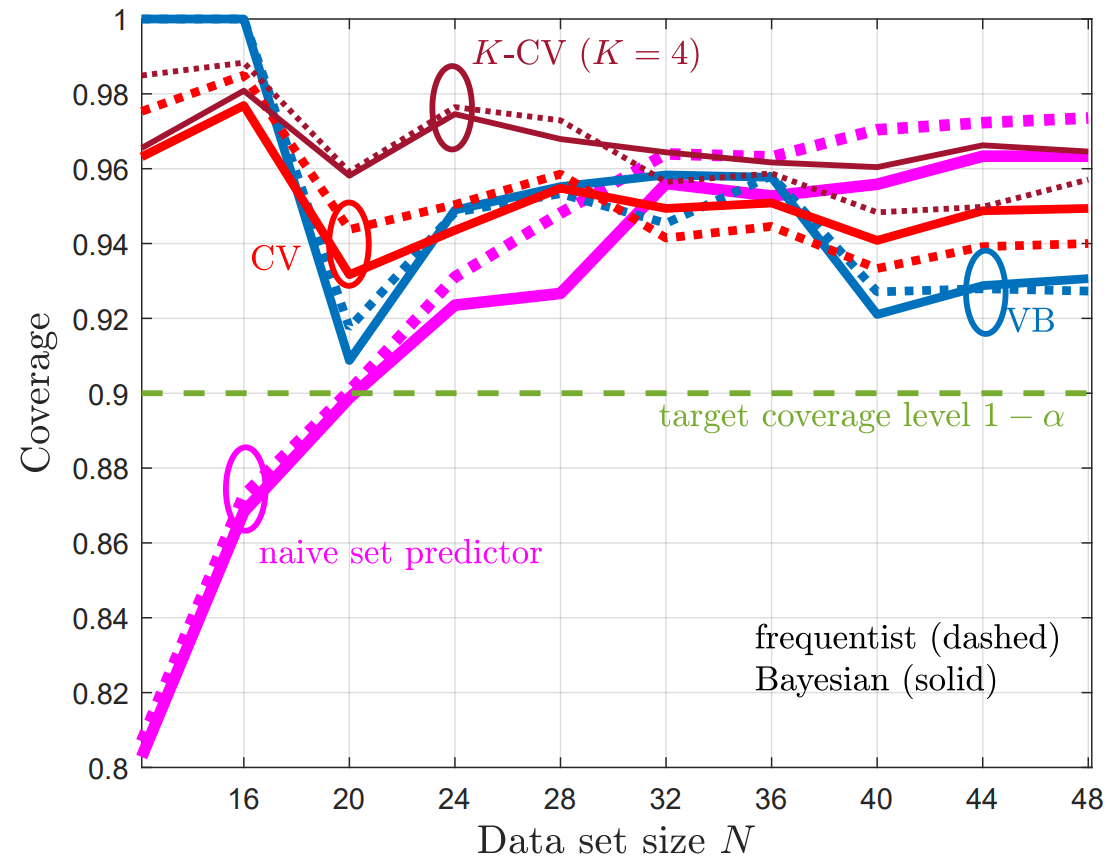
In our recent work, to appear in IEEE Journal of Selected Topics in Signal Processing, we study for the first time leveraging online conformal prediction (CP) for providing assumptions-free guarantees on the safety level of the attempted candidate solutions, while enabling any non-zero target safety violation level. As shown in Fig. 2, we introduce Safe-BOCP that models objective function and constraint function by using independent Gaussian processes (GPs) as surrogate models, calibrating the credible intervals constructed for safe sets adaptively based on the observation history via online CP [3] [4]. The key mechanism is to use safety feedback, in the form of a well-designed safety error signal, on the reliability of past decisions to adjust the post-processing of probabilistic surrogate model’s outputs. In contrast to previous safe BO methods assuming RKHS properties of the constraint function to ensure a strict safety guarantee, Safe-BOCP adopts a “caution-increasing” back-off strategy that compensates for the uncertainty on the boundaries of the safe regions without any assumptions.
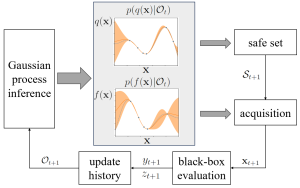
Fig. 2. Block diagram of the main steps including safe set creation, producing the safe set, and of acquisition, selecting the next iterate.
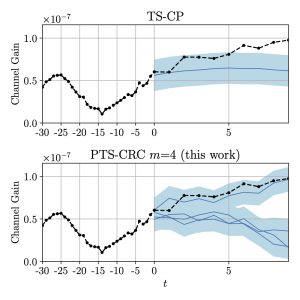
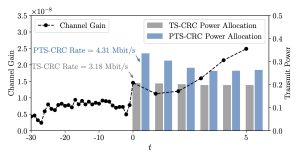
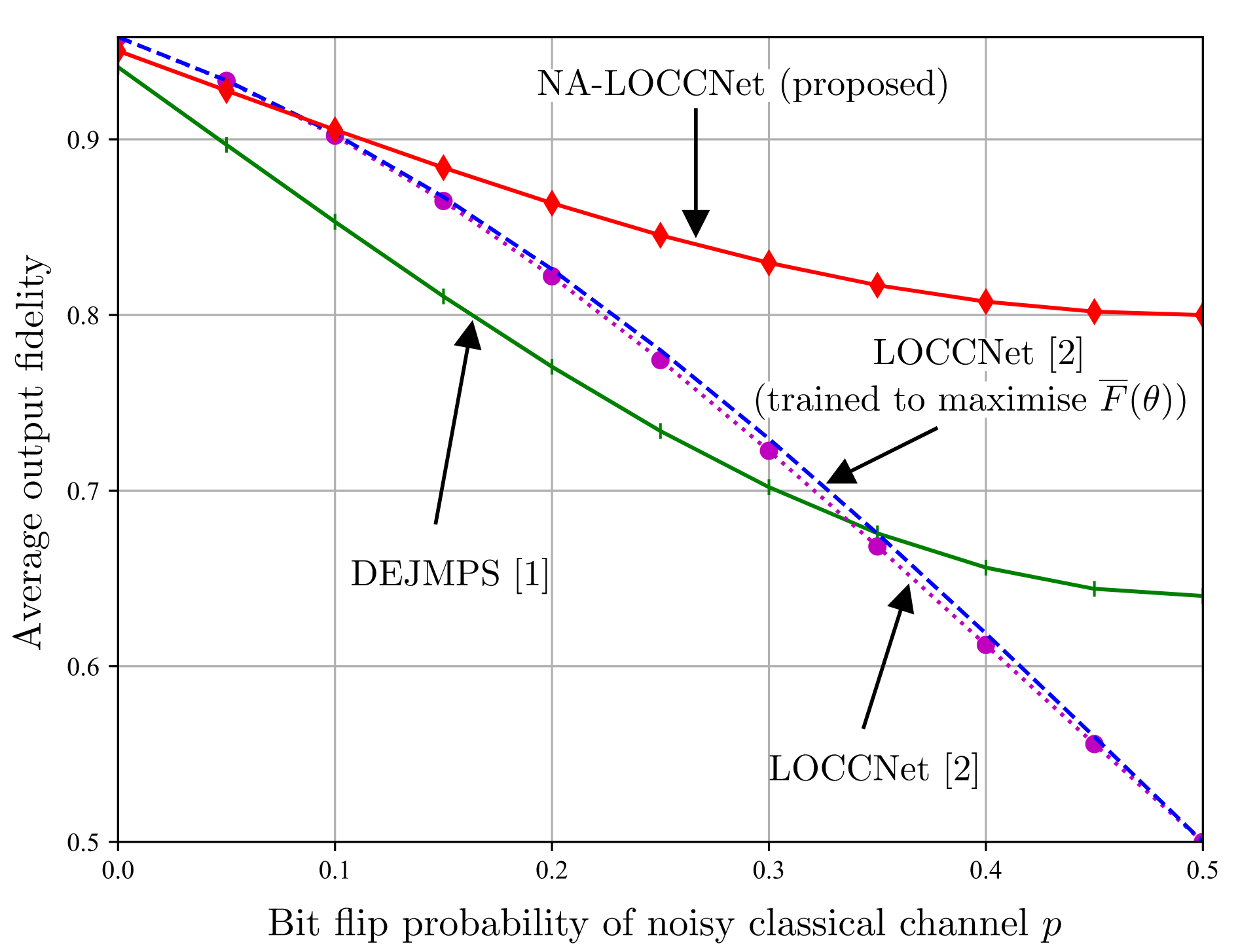
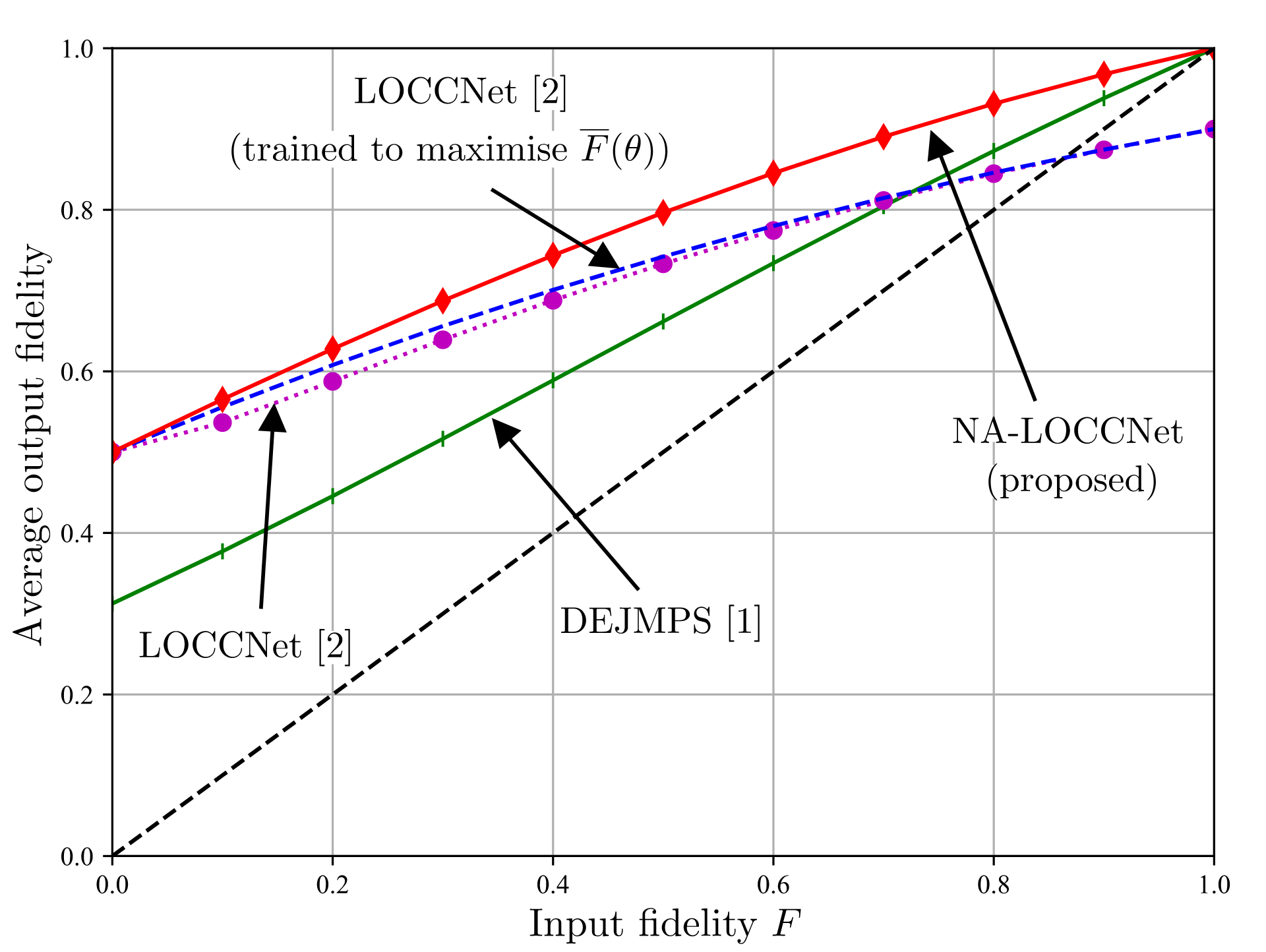
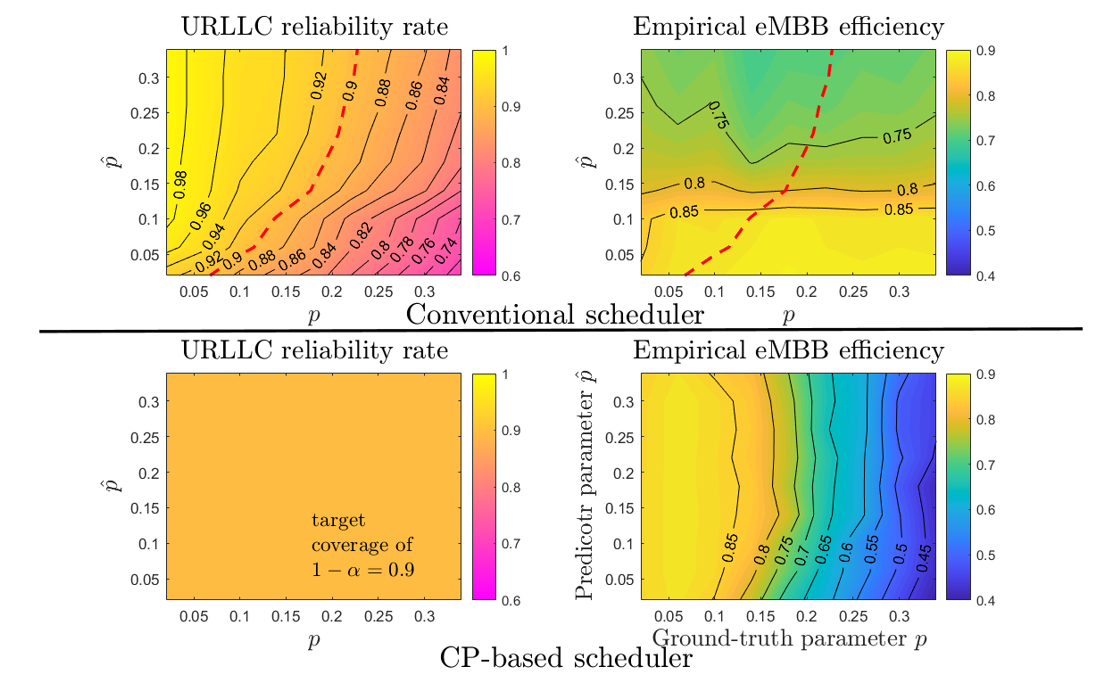
Experiments
We compare Safe-BOCP with the state-of-the-art SAFEOPT in a safe movie recommendation problem and plug flow reactor (PFR) optimization problem. Fig. 3 plots the histograms of the ratings across all selected movies during the optimization procedure with varying target violation rates, showing that SAFEOPT does not meet the safety requirement (red dashed line) while D-SAFE-BOCP can correctly control the fraction of unsafe movies. As shown in Fig. 4, P-SAFE-BOCP is seen to meet the target reliability level irrespective of observation noise power, while SAFEOPT can only achieve it when the observation noise power is sufficiently large.
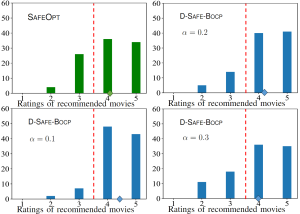
Fig. 3. Histograms of the ratings of recommended movies by SAFEOPT, as well by D-SAFE-BOCP under different target violation rates.
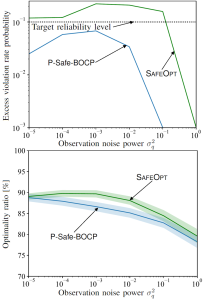
Fig. 4. Probability of excessive violation rate (top) and optimality ratio (bottom) as a function of constraint observation noise power.
References
[1] Y. Sui, A. Gotovos, J. Burdick, and A. Krause, “Safe exploration for optimization with Gaussian processes,” in Proceedings of International Conference on Machine Learning, Lille, France, 2015.
[2] F. Berkenkamp, A. Krause, and A. P. Schoellig, “Bayesian optimization with safety constraints: Safe and automatic parameter tuning in robotics,” Machine Learning, pp. 1–35, 2021.
[3] I. Gibbs and E. Candes, “Adaptive conformal inference under distribution shift,” in Proceedings of Advances in Neural Information Processing Systems, Virtual, 2021.
[4] S. Feldman, L. Ringel, S. Bates, and Y. Romano, “Achieving risk control in online learning settings,” Transactions on Machine Learning Research, 2023.

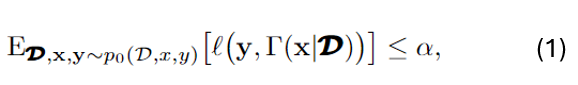
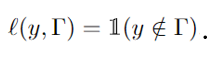
Recent Comments