Motivation
The control of dynamical systems is the backbone of modern technologies, ranging from industrial processes to autonomous vehicles. In many of these scenarios, systems must be controlled while satisfying a set of safety and reliability constraints with respect to the unknown evolution of a target process. For example, as illustrated in Figure 1, autonomous vehicles or unmanned aerial vehicles (UAVs) must plan their trajectory while maintaining a safe distance from other vehicles or obstacles. To this end, predictions about the future evolution of the system must be used. In this context, a primary challenge is to ensure safety and reliability in the face of predictions that are often uncertain.
Figure 1: UAV tracking problem, an example of model predictive control in which the UAV must plan its path based on the unknown evolution of the object to be tracked.
Probabilistic Time Series-Conformal Risk Prediction
To support the deployment of reliable control mechanisms for dynamical system, in our work we have recently proposed probabilistic time series-conformal risk prediction (PTS-CRC). PTS-CRC is a novel post-hoc calibration procedure that operates on the predictions produced by any pre-designed probabilistic forecaster to yield reliable time series prediction sets. As illustrated in Figure 2, PTS-CRC generates predictive sets based on an ensemble of multiple prototype trajectories sampled from the probabilistic model, supporting the efficient representation of forking uncertainties. This contrasts with previous solutions that apply Conformal Prediction[1] to deterministic predictors (TS-CP)[2], which are bounded to produce compact prediction sets. Furthermore, sets produced by PTS-CRC can be calibrated to satisfy a wide array of reliability definitions, beyond the standard one of coverage.
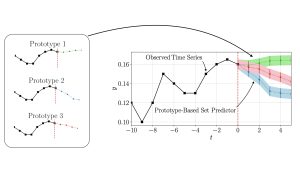
Figure 2: Construction of a prototype-based set predictor based on 3 prototypical sequences.
PTS-CRC Based Model Predictive Control
Based on the reliability properties of PTS-CRC predictions, we devise a novel Model Predictive Control (MPC) framework that addresses open-loop and closed-loop control problems under general average constraints on the quality or safety of the control policy. The key idea is to derive the control by replacing constraints that depend on the unknown dynamics of the target process with those depending on the predictive sets output by PTS-CRC. The reliability requirements of PTS-CRC predictions translate into reliability requirements for the original control problem.
Experiments
We apply PTS-CRC-based MPC to wireless networking problems, specifically focusing on a scenario where a base station must modulate its future power allocation based on the unknown evolution of channel conditions. For instance, we address the challenge of controlling transmit power to maximize the communication rate at an unlicensed user while adhering to a safety requirement, expressed as the maximum interference experienced by a licensed user. By employing PTS-CRC, we can replace the unknown system evolution with efficient multimodal predictive sets that more effectively capture multimodal channel evolution compared to TS-CP (Figure 3). As exemplified in Figure 4, PTS-CRC-based power control leads to power allocations that achieve a higher communication rate compared to TS-CP.
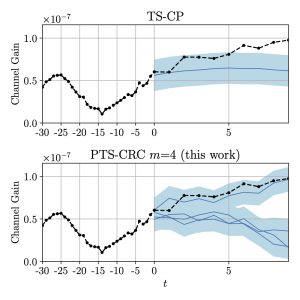
Figure 3: Comparison between the prediction sets of TS-CP and PTS-CRC for the problem of channel gain evolution forecasting.
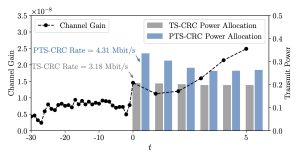
Figure 4: Comparison between the power control solution obtained using PTS-CRC and TS-CP based MPC.
References
[1] Vovk, Vladimir, Alexander Gammerman, and Glenn Shafer. “Algorithmic learning in a random world,” Vol. 29. New York: Springer, 2005.
[2] Stankeviciute, Kamile, Ahmed M Alaa, and Mihaela van der Schaar. “Conformal time-series forecasting.” Advances in neural information processing systems 34, 2021.
[3] Zecchin, Matteo, Sangwoo Park, and Osvaldo Simeone. “Forking Uncertainties: Reliable Prediction and Model Predictive Control with Sequence Models via Conformal Risk Control.” arXiv preprint arXiv:2310.10299, 2023.

Leave a Reply