A quantum computer can be programmed to carry out a given functionality in different ways, including the direct engineering of pulse sequences, the design of parametric quantum circuits via quantum machine learning (QML) [1], the use of adaptive measurements on cluster states, and the optimization of a program state operating on a fixed quantum processor. A fundamental result derived in [2] states there is no universal programmable quantum processor that operates with finite-dimensional program states. Since a quantum processor is universal if it can implement any quantum operation, this conclusion implies that the exact simulation of an arbitrary quantum channel on a single programmable quantum processor is impossible. This, in turn, highlights the importance of developing tools for the optimization of quantum programs. Reference [3] addressed the problem of approximately simulating a given quantum channel using a finite-dimensional program state.
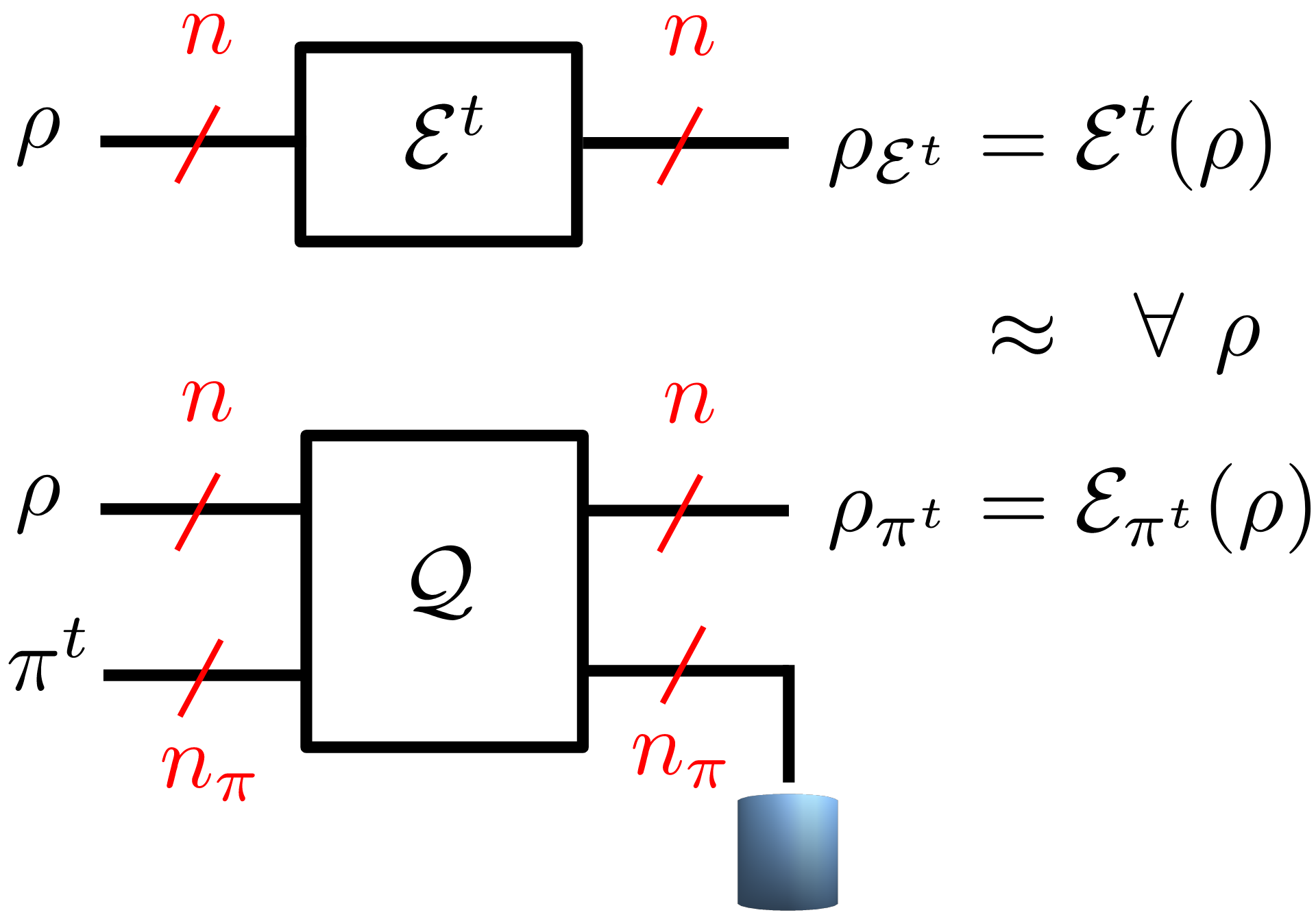
Fig. 1: Fig. 1. Time-varying quantum channel ε^t (top) and its simulation ε_(π^t ) via a programmable quantum processor Q controlled by the time-varying program state π^t (bottom).
In our recent work, presented at IEEE ITW 2023, we study the more challenging setting illustrated in Fig. 1, in which the channel to be simulated varies over time. We adopt a worst-case formulation in which the channel variation is arbitrary and chosen by “nature” in a possibly adversarial way. To study this setting, we propose to adopt the framework of online convex optimization [4], which provides tools to track the optimal solution of time-varying convex problems. We specifically develop and analyze an online mirror descent algorithm over the space of positive definite matrices, yielding a matrix exponentiated gradient descent (MEGD) [5]. We prove that the regret of MEGD with respect to an optimized fixed program state is sublinear in time.
Experiments
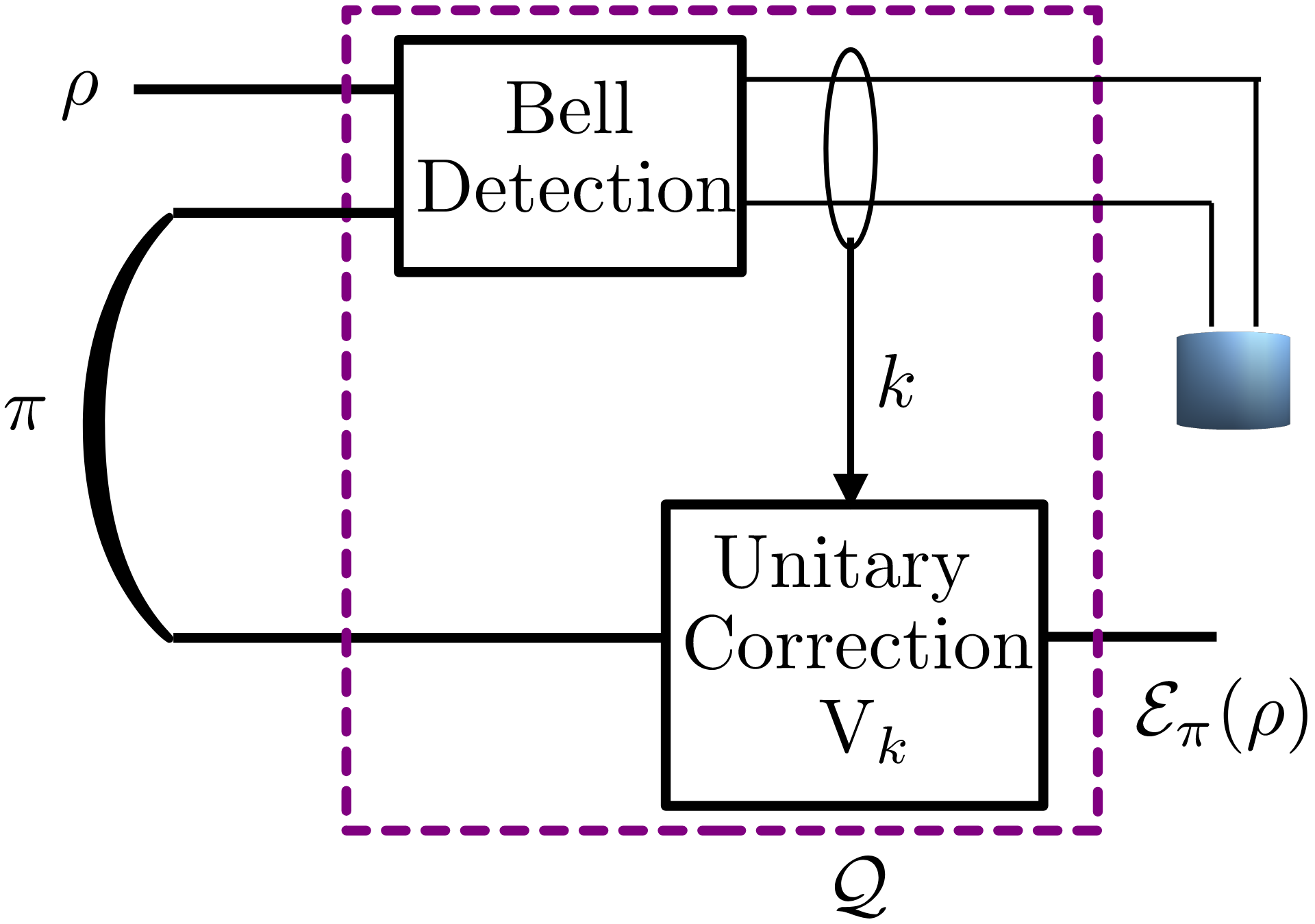
Fig. 2: Generalized teleportation processor as a programmable processor Q
operating on one input qubit (n=1) and on a two-qubit program state π
(n_π=2).
We conduct experiments by adopting the generalized teleportation processor (GTP), shown in Fig. 2, as the programmable quantum processor. GTP can simulate exactly the class of teleportation-covariant channels, modeling Pauli and erasure channels, and is operated here in an adversarial setting with time varying dephasing channels. Fig.3 plots the normalized regret as a function of time T. We observe that, MEGD is able to obtain a normalized regret that decreases sublinearly with T, hence approaching the performance of the reference program that would have been optimal in hindsight.
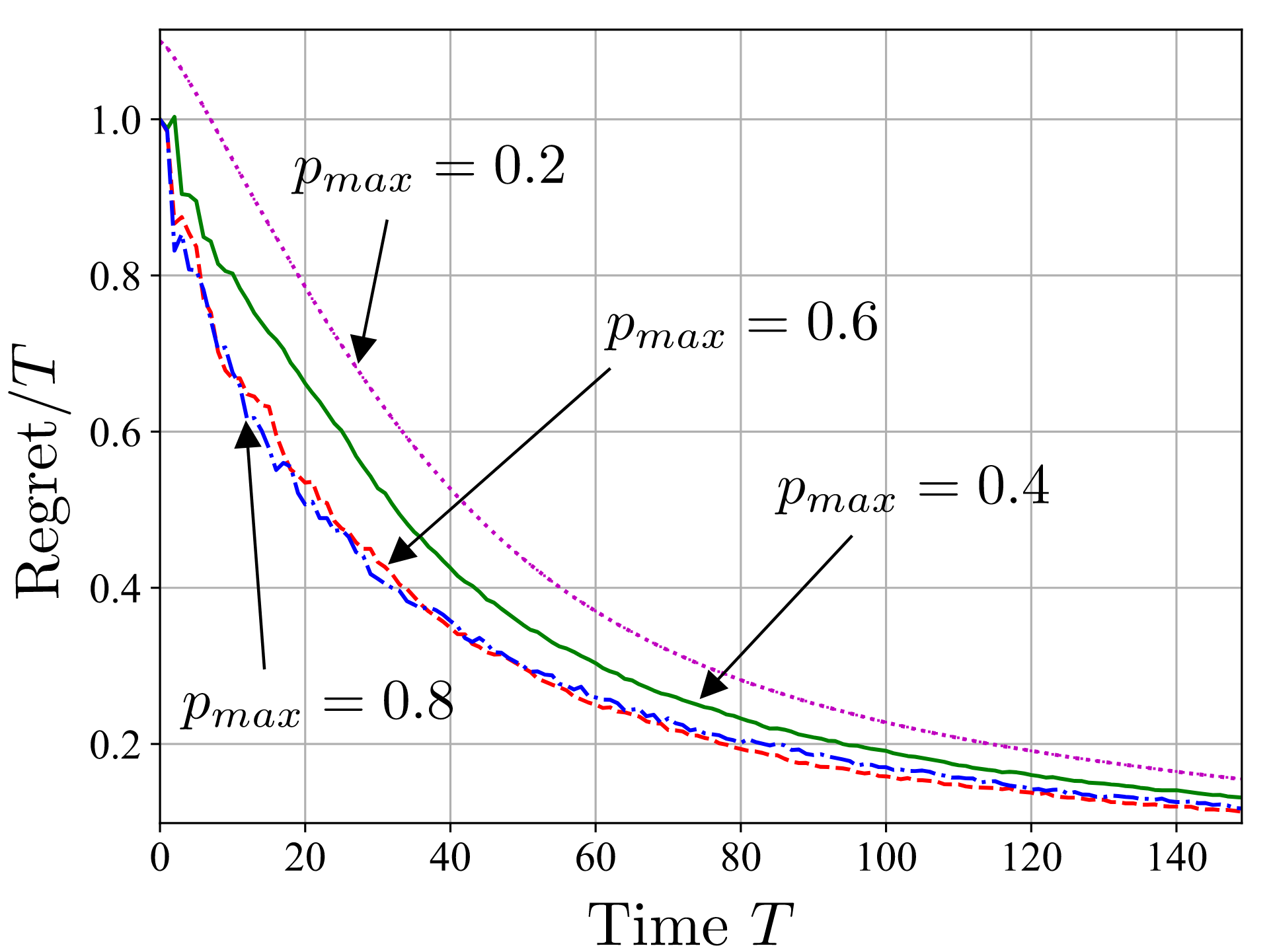
Fig. 3: Normalized regret as a function of time T for MEGD when simulating a time-varying dephasing channel with dephasing probabilities drawn independently and uniformly at each time in the interval [0.2,p_max) (setting p_max=0.2 models a constant channel).
[1] O. Simeone, “An introduction to quantum machine learning for engineers”,
Foundations and Trends in Signal Processing, vol. 16, no. 1-2, pp. 1–223, 2022.
[2] M. A. Nielsen and I. L. Chuang, “Programmable quantum gate arrays”, Phys. Rev. Lett., vol. 79, pp. 321–324, Jul 1997.
[3] L. Banchi, J. Pereira, S. Lloyd, and S. Pirandola, “Convex optimization of programmable quantum computers”, npj Quantum Information, vol. 6, no. 1, pp. 1–10, 2020.
[4] F. Orabona, “A modern introduction to online learning”, CoRR, vol. abs/1912.13213, 2019.
[5] K. Tsuda, G. Ratsch, and M. K. Warmuth, “Matrix exponentiated gradient updates for on-line learning and Bregman projection”, Journal of Machine Learning Research, vol. 6, no. 34, pp. 995–1018, 2005.

Leave a Reply