Motivation

Hyperparameter optimization (HPO) is essential in tuning artificial intelligence (AI) models for practical engineering applications, as it governs model performance across varied deployment scenarios. Conventional HPO techniques such as random search and Bayesian optimization often focus on optimizing average performance without providing statistical guarantees, which can be limiting in high-stakes engineering tasks where system reliability is crucial. The learn-then-test (LTT) method [1], introduced in recent research, offers statistical guarantees on the average risk associated with selected hyperparameters. However, in fields like wireless networks and real-time systems, designers frequently need assurance that a specified quantile of performance will meet reliability thresholds.

To address this need, our proposed method, Quantile Learn-Then-Test (QLTT), extends LTT to offer statistical guarantees on quantiles of risk rather than just the average. This quantile-based approach provides greater robustness in real-world applications where it’s critical to control risk-aware objectives, ensuring that the system meets performance goals in a specified fraction of scenarios.

Quantile Learn-Then-Test (QLTT)

LTT, as introduced in [1], guarantees that the average risk remains within a defined threshold with high probability. However, many real-world applications require tighter control over performance measures. For instance, in cellular network scheduling, system designers may need to ensure that key performance indicators (KPIs) like latency and throughput stay within acceptable limits for a majority of users, not just on average.

Our approach, QLTT, extends LTT to provide guarantees on any specified quantile of risk. Specifically, QLTT selects hyperparameters that ensure a predefined quantile of the risk distribution meets a target threshold. This probabilistic guarantee, based on quantile risk control, better aligns with the needs of applications where performance variability is critical.

Methodology

QLTT builds on LTT’s multiple hypothesis testing framework, incorporating a quantile-specific confidence interval, obtained using [2], to achieve guarantees on the desired quantile of risk. The method takes a set of hyperparameter candidates and identifies those that meet the desired quantile threshold with high probability, enhancing reliability beyond what is possible through average risk control alone. This quantile-based approach enables QLTT to adapt to varying risk tolerance levels, making it versatile for different engineering contexts.

Experiments

To demonstrate QLTT’s effectiveness, we applied it to a radio access scheduling problem in wireless communication [3]. Here, the task was to allocate limited resources among users with different quality of service (QoS) requirements, ensuring that latency requirements were met for the vast majority of users in real-time.

Our experimental results highlight QLTT’s advantage over LTT with respect to quantile control. While both methods controlled the average risk effectively, only QLTT managed to limit the higher quantiles of the risk distribution, reducing instances where latency exceeded critical thresholds.

The following figure compares the distributions of packet delays for conventional LTT and QLTT for a test run of the simulation. While LTT shows considerable variance, with some instances exceeding the desired threshold, QLTT consistently meets the reliability requirements by providing tighter control over risk quantiles.

Conclusion

QLTT extends the applicability of LTT by providing hyperparameter sets with guarantees on quantiles of a risk measure, thus offering a more rigorous approach to HPO for risk-sensitive engineering applications. Our experiments confirm that QLTT effectively addresses scenarios where quantile risk control is required, providing a robust solution to ensure high-confidence performance across diverse conditions.

Future work may explore expanding QLTT to more complex settings, such as other types of risk functionals and broader engineering challenges. By advancing risk-aware HPO, QLTT represents a significant step toward reliable, application-oriented AI optimization in critical industries.

References

[1] Angelopoulos, A.N., Bates, S., Candès, E.J., Jordan, M.I., & Lei, L. (2021). Learn then test: Calibrating predictive algorithms to achieve risk control. arXiv preprint arXiv:2110.01052.

[2] Howard, S.R., & Ramdas, A. (2022). Sequential estimation of quantiles with applications to A/B testing and best-arm identification. Bernoulli, 28(3), 1704–1728.

[3] De Sant Ana, P.M., & Marchenko, N. (2020). Radio Access Scheduling using CMA-ES for Optimized QoS in Wireless Networks. IEEE Globecom Workshops (GC Wkshps), pp. 1-6.

Motivation

In machine learning, the information bottleneck (IB) problem [1] is a critical framework used to extract compressed features that retain sufficient information for downstream tasks. However, a major challenge lies in selecting hyperparameters that ensure the learned features comply with information-theoretic constraints. Current methods rely on heuristic tuning without providing guarantees that the chosen features satisfy these constraints. This lack of rigor can lead to suboptimal models. For example, in the context of language model distillation, failing to enforce these constraints may result in the distilled model losing important information from the teacher model.

Our proposed method, “IB via Multiple Hypothesis Testing” (IB-MHT), addresses this issue by introducing a statistically valid solution to the IB problem. We ensure that the features learned by any IB solver meet the IB constraints with high probability, regardless of the dataset size. IB-MHT builds on Pareto testing [2] and learn-then-test (LTT) [3] methods to wrap around existing IB solvers, providing statistical guarantees on the information bottleneck constraints. This approach offers robustness and reliability compared to conventional methods that may not meet these constraints in practice.

IB-MHT

In the traditional IB framework, we aim to minimize the mutual information between the input data X and a compressed representation T, while ensuring that T retains sufficient information about a target variable Y. This is expressed mathematically as minimizing I(X;T) under the constraint that I(T;Y) exceeds a certain threshold. In practice, though, solving this problem often relies on tuning a Lagrange multiplier or hyperparameters to balance the compression of T and the information retained about Y. These approaches do not guarantee that the solution will meet the required information-theoretic constraints.

To overcome this, IB-MHT introduces a probabilistic approach where we wrap around any existing IB solver to ensure that the learned features satisfy the IB constraint with high probability. By leveraging Pareto testing, IB-MHT identifies the optimal hyperparameters through a family-wise error rate (FWER) testing mechanism, ensuring that the final solution is statistically sound.

Experiments

To validate the effectiveness of IB-MHT, we conducted experiments on both classical and deterministic IB [4] formulations. One experiment was performed on the MNIST dataset, where we applied IB-MHT to ensure that the learned representations met the IB constraints with high probability. In another experiment, we applied IB-MHT to the task of distilling language models, transferring knowledge from a large teacher model to smaller student model. We demonstrated that IB-MHT successfully guarantees that the compressed features retain sufficient information about the target variable. Compared to conventional IB methods, IB-MHT showed significant improvements in both the reliability and consistency of the learned representations, with reduced variability in the mutual information estimates.

The following figure illustrates the difference between the performance of conventional IB solvers and IB-MHT in a classical IB setup. While the conventional solver shows a wide variance in the mutual information values, IB-MHT provides tighter control, ensuring that the learned representation T meets the desired information-theoretic constraints.

Conclusion

IB-MHT introduces a reliable, statistically valid solution to the IB problem, addressing the limitations of heuristic hyperparameter tuning in existing methods. By guaranteeing that the learned features meet the required information-theoretic constraints with high probability, IB-MHT enhances the robustness and performance of IB solvers across a range of applications. Future work can explore extending IB-MHT to continuous variables and applying similar techniques to other information-theoretic objectives such as convex divergences.

References

[1] Naftali Tishby, Fernando Pereira, and William Bialek. The information bottleneck method. Proceedings of the 37th Allerton Conference on Communication, Control, and Computing, 2001.

[2] Laufer-Goldshtein, Ben, Ariel Fisch, Regina Barzilay, and Tommi Jaakkola. Efficiently controlling multiple risks with Pareto testing. International Conference on Learning Representations, 2023.

[3] Angelopoulos, Anastasios N., Stephen Bates, Emmanuel J. Candès, Michael I. Jordan, and Lucas Lei. Learn then test: Calibrating predictive algorithms to achieve risk control. arXiv preprint arXiv:2110.01052, 2021.

[4] Strouse, Daniel, and David Schwab. The deterministic information bottleneck. Neural Computation, 2017.

Context and Motivations

Neuromorphic processing units (NPUs), such as Intel’s Loihi or BrainChip’s Akida, leverage the sparsity of temporal data to reduce processing energy by activating a small subset of neurons and synapses at each time step. When deployed for split computing in edge-based systems, remote NPUs, each carrying out part of the computation, can reduce the communication power budget by communicating asynchronously using sparse impulse radio (IR) waveforms [1-2], a form of ultra-wide bandwidth (UWB) spread-spectrum signaling.

However, the power savings afforded by sparse transmitted signals are limited to the transmitter’s side, which can transmit impulsive waveforms only at the times of synaptic activations. The main contributor to the overall energy consumption remains the power required to maintain the main radio on.

Architecture

To address this architectural problem, as seen in the figure above, our recent work [3-4] proposes a novel architecture that integrates a wake-up radio mechanism within a split computing system consisting of remote, wirelessly connected, NPUs. In the proposed architecture, the NPU at the transmitter side remains idle until a signal of interest is detected by the signal detection module. Subsequently, a wake-up signal (WUS) is transmitted by the wake-up transmitter over the channel to the wake-up receiver, which activates the main receiver. The IR transmitter modulates the encoded signals from the NPU, and sends them to the main receiver. The NPU at the receiver side then decodes the received signals and make an inference decision.

Digital twin-aided design methodology with reliability guarantee

A key challenge in the design of a wake-up radios is the selection of thresholds for sensing and WUS detection, and decision making (three λ’s in the figure above). A conventional solution would be to calibrate the thresholds via on-air testing, trying out different thresholds via testing on the actual physical system. On-air calibration would be expensive in terms of spectral resources, and there is generally no guarantee that the selected thresholds would provide desirable performance levels for the end application.

To address this design problem, as illustrated in the figure below, this work proposes a novel methodology, dubbed DT-LTT,  that leverages the use of a digital twin, i.e., a simulator, of the physical system, coupled with a sequential statistical testing approach that provides theoretical reliability guarantees. Specifically, the digital twin is leveraged to pre-select a sequence of hyperparameters to be tested using on-air calibration via Learn then Test (LTT) [5]. The proposed DT-LTT calibration procedure is proved to guarantee reliability of the receiver’s decisions irrespective of the fidelity of digital twin and of the data distribution.

Experiment

We compare the proposed DT-LTT calibration method with conventional neuromorphic wireless communications without wake-up radio, conventional LTT without a digital twin, and DT-LTT with an always-on main radio system. As shown in the figure below, the conventional calibration scheme fails to meet the reliability requirement, while the basic LTT scheme selects conservative hyperparameters, often including all classes in the predicted set, which results in zero expected loss. In contrast, the proposed DT-LTT schemes are guaranteed to meet the probabilistic reliability requirement.

References

[1] J. Chen, N. Skatchkovsky and O. Simeone, “Neuromorphic Wireless Cognition: Event-Driven Semantic Communications for Remote Inference,” in IEEE Transactions on Cognitive Communications and Networking, vol. 9, no. 2, pp. 252-265, April 2023,.

[2] J. Chen, N. Skatchkovsky and O. Simeone, “Neuromorphic Integrated Sensing and Communications,” in IEEE Wireless Communications Letters, vol. 12, no. 3, pp. 476-480, March 2023.

[3] J. Chen, S. Park, P. Popovski, H. V. Poor and O. Simeone, “Neuromorphic Split Computing with Wake-Up Radios: Architecture and Design via Digital Twinning,” in IEEE Transactions on Signal Processing, Early Access, 2024.

[4] J. Chen, S. Park, P. Popovski, H. V. Poor and O. Simeone, “Neuromorphic Semantic Communications with Wake-Up Radios,” Proc. IEEE 25th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Lucca, Italy, pp. 91-95, 2024.

[5] Angelopoulos, Anastasios N., et al. “Learn then test: Calibrating predictive algorithms to achieve risk control,” arXiv preprint arXiv:2110.01052, 2021.

Motivation

In many online decision-making settings, ensuring that predictions are well-calibrated is crucial for the safe operation of systems. One way to achieve calibration is through adaptive risk control, which adjusts the uncertainty estimates of a machine learning model based on past feedback [1]. This method guarantees that the calibration error over an arbitrary sequence is controlled and that, in the long run, the model becomes statistically well-calibrated if the data points are independently and identically distributed [2]. However, these schemes only ensure calibration when averaged across the entire input space, raising concerns about fairness and robustness. For instance, consider the figure below, which depicts a tumor segmentation model calibrated to identify potentially cancerous areas. If the model is calibrated using images from different datasets, marginal calibration may be achieved by prioritizing certain subpopulations at the expense of others.

A tumor segmentation model is calibrated using data from two sources to ensure that the marginal false negative rate (FNR) is controlled. However, as shown on the right, the error rate for one source is significantly lower than for the other, leading to unfair performance across subpopulations.

Localized Adaptive Risk Control

To address this issue, our recent work at NeurIPS 2024 proposes a method to localize uncertainty estimates by leveraging the connection between online learning in reproducing kernel Hilbert spaces [3] and online calibration methods. The key idea behind our approach is to use feedback to adjust a model’s confidence levels only in regions of the input space that are near observed data points. This allows for localized calibration, tailoring uncertainty estimates to specific areas of the input space. We demonstrate that, for adversarial sequences, the number of mistakes can be controlled. More importantly, the scheme provides asymptotic guarantees that are localized, meaning they remain valid under a wide range of covariate shifts, for instance those induced by considering certain subpopulation of the data.

Experiments

Comparison between the coverage map obtained using adaptive risk control (on the left) and localized adaptive risk control (on the right). Adaptive risk control is unable to deliver uniform coverage across the deployment areas, leading to large regions where the SNR level is unsatisfactory. In contrast, localized adaptive risk control is capable of guaranteeing a more uniform SNR level, improving the overall system coverage.

To demonstrate the fairness improvements of our algorithm, we conducted a series of experiments using standard machine learning benchmarks as well as wireless communication problems. Specifically, in the wireless domain, we considered the problem of beam selection based on contextual information. Here, a base station must select a subset of communication beam vectors to guarantee a level of signal-to-noise ratio (SNR) across a deployment area. Standard calibration methods like adaptive risk control (on the left) result in substantial SNR variation across the area, creating regions where communication is impossible. In contrast, our localized adaptive risk control scheme (on the right) enables the base station to calibrate the beam selection algorithm to match the local uncertainty, providing more uniform coverage throughout the deployment area.

References

[1] Isaac Gibbs and Emmanuel Candes. Adaptive conformal inference under distribution shift. Advances in Neural Information Processing Systems, 34 (2021).

[2] Anastasios Nikolas Angelopoulos, Rina Barber, Stephen Bates. Online conformal prediction with decaying step sizes. Proceedings of the 41st International Conference on Machine Learning. (2024).

[3] Jyrki Kivinen, Alex Smola and Robert C. Williamson. Online Learning with Kernels. Advances in Neural Information Processing Systems, 14 (2001)

Motivation

Conformal risk control (CRC) [1] [2] is a recently proposed technique that applies post-hoc to a conventional point predictor to provide calibration guarantees. Generalizing conformal prediction (CP) [3], with CRC, calibration is ensured for a set predictor that is extracted from the point predictor to control a risk function such as the probability of miscoverage or the false negative rate. The original CRC requires the available data set to be split between training and validation data sets. This can be problematic when data availability is limited, resulting in inefficient set predictors. In [4], a novel CRC method is introduced that is based on cross-validation, rather than on validation as the original CRC. The proposed cross-validation CRC (CV-CRC) allows for the control of a broader range of risk functions, while proved to offer theoretical guarantees on the average risk of the set predictor, and reduced average set size with respect to CRC when the available data are limited.

Cross-Validation Conformal Risk Control

The objective of CRC is to design a set predictor with a mean risk no larger than a predefined level α, i.e.,

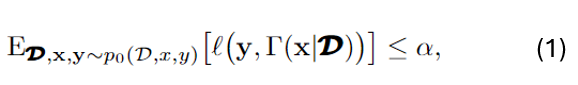
with test data input-label pair (x,y), and a set of N data pairs D.

The risk is defined between the  true label y and a predictive set Γ of labels.

VB-CRC generalizes VB-CP [2] in the sense it allows the risk taking arbitrary form under technical conditions such as boundness and monotonicity in the set. VB-CP is resorted when VB-CRC considers the special case of the miscoverage risk

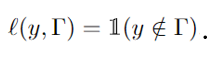
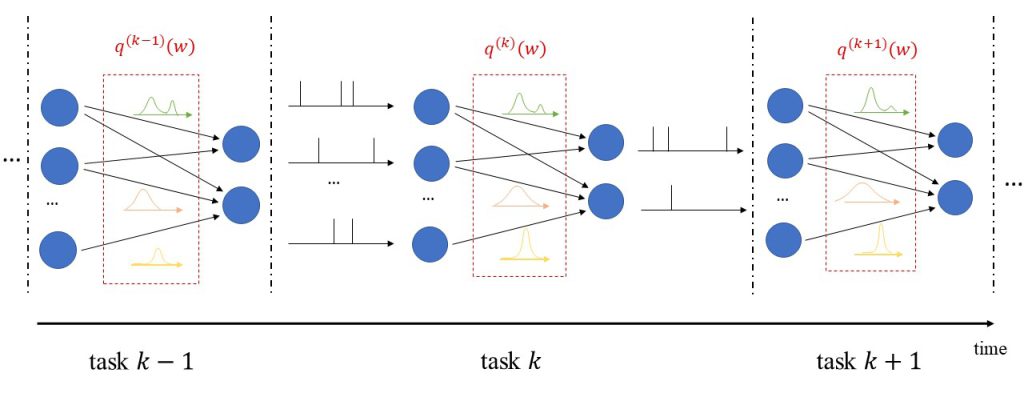
In this work, we introduce CV-CRC, which is a cross-validation-based version of VB-CRC. In a similar manner how CV-CP [5] generalizes VB-CP, CV-CRC generalizes VB-CRC. See Fig. 1 for illustration.

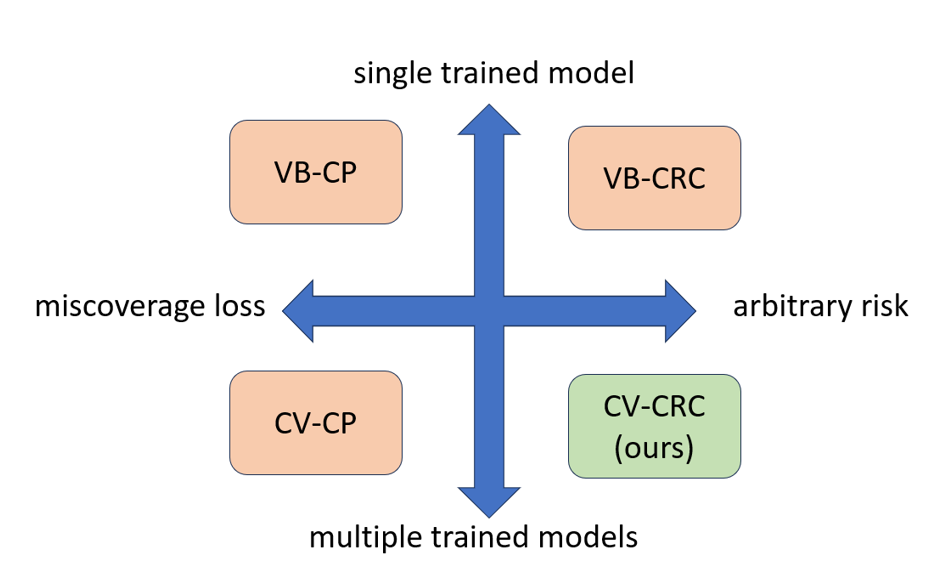
Fig. 1. (top) validation-based CRC (bottom) the proposed method, CV-CRC.

In the top panel of Fig. 2, VB-CRC is shown as the outcome of available data split into training data and validation data. The former is used to train a model, while the latter is used to post process and control a threshold λ. Upon test input x, a predictive set Γ of labels y’s is formed. In the bottom panel, CV-CRC is illustrated as a generalization. Available data is split K≤N folds, and K leave-fold-out models are trained. Then, K predictive sets are formed and merged via a threshold that is set via the trained models and the left-fold-out data.

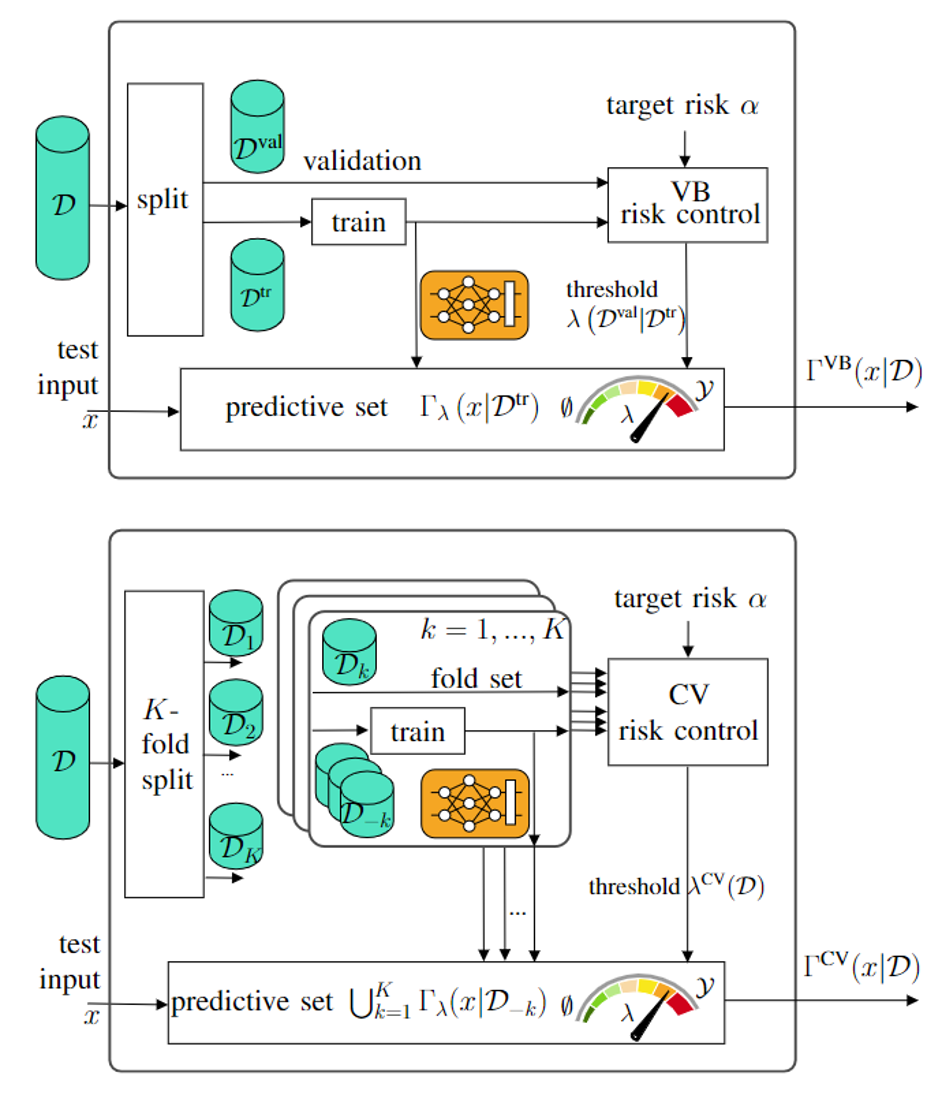
Fig. 2. (top) validation-based CRC (bottom) the proposed method, CV-CRC.

Experiments

To illustrate the main theorem that the risk guarantee (1) is met, while the average set sizes are expected to reduce, two experiments were conducted. The first is vector regression using maximum-likelihood learning, and is shown in Fig. 3.

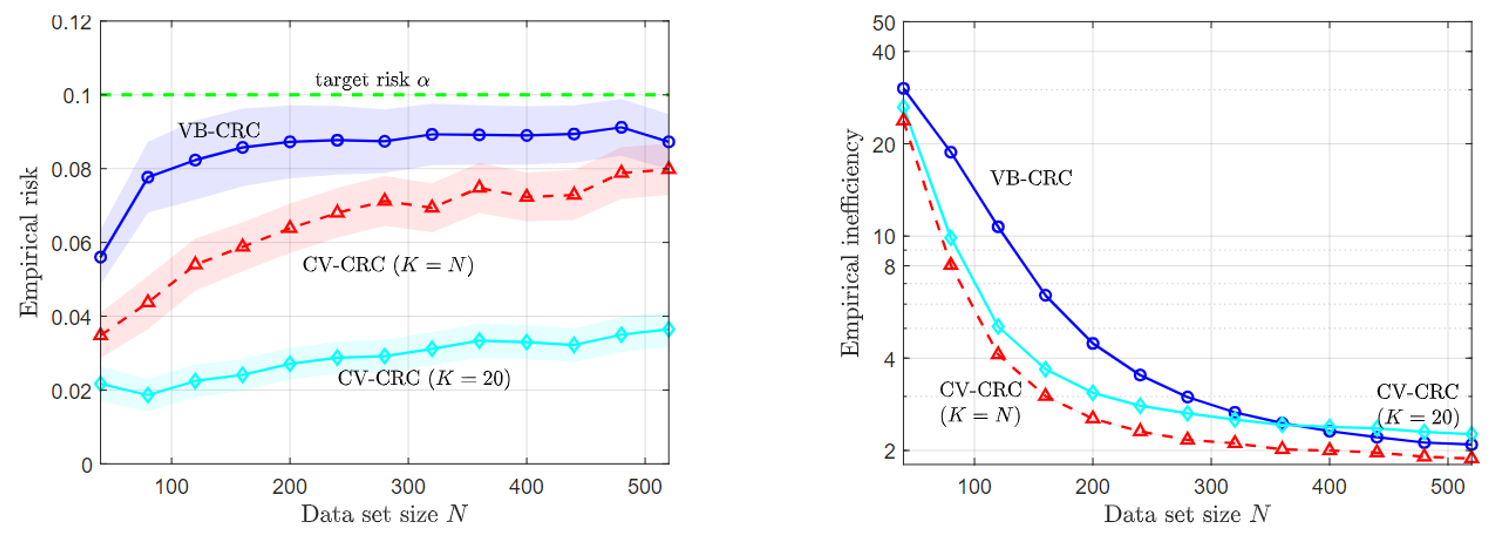
Fig. 3. VB-CRC and CV-CRC for the vector regression problem.

The second problem is a temporal point process prediction, where a point process set predictor aims to predict sets that contain future events of a temporal process with false negative rate of no more than a predefined α. As can be seen, in both problems, CV-CRC is shown to be more data-efficient in the small data regime, while holding the risk condition (1).

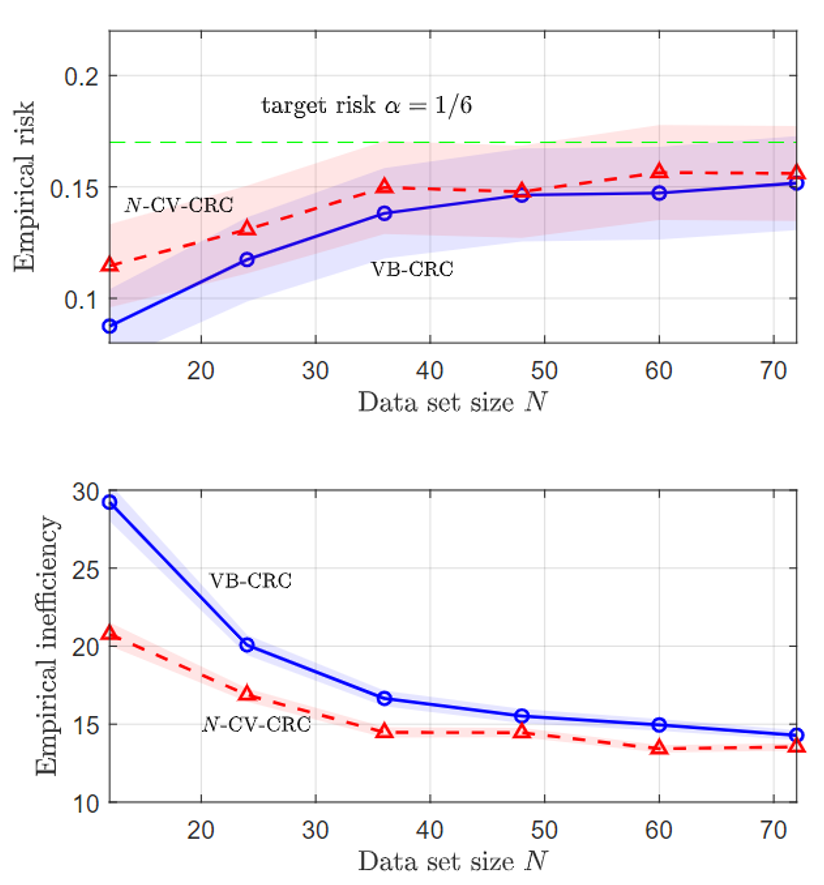
Fig. 4. VB-CRC and CV-CRC for the temporal point process prediction problem.

Full details can be found at ISIT preprint [4].

References

[1] A. N. Angelopoulos, S. Bates, A. Fisch, L. Lei, and T. Schuster, “Conformal Risk Control,” in The Twelfth International Conference on Learning Representations, 2024.

[2] S. Feldman, L. Ringel, S. Bates, and Y. Romano, “Achieving Risk Control in Online Learning Settings,” Transactions on Machine Learning Research, 2023.

[3] V. Vovk, A. Gammerman, and G. Shafer, Algorithmic Learning in a Random World. Springer, 2005, springer, New York.

[4] K. M. Cohen, S. Park, O. Simeone, and S. Shamai Shitz, “Cross-Validation Conformal Risk Control,” accepted to IEEE International Symposium on Information Theory Proceedings (ISIT2024), July 2024.

[5] R. F. Barber, E. J. Candes, A. Ramdas, and R. J. Tibshirani, “Predictive Inference with the Jackknife+,” The Annals of Statistics, vol. 49, no. 1, pp. 486–507, 2021.

Motivation

Servicing ultra-reliable and low-latency communication (URLLC) traffic typically calls for a pre-emptive allocation of resources in order to meet stringent delay constraints. A conservative static allocation of resources for URLLC may guarantee desired levels of reliability and latency, but this comes at the expense of other services, most notably enhanced mobile broadband (eMBB), which cannot use the resources reserved for URLLC. A dynamic allocation of resources, while potentially more efficient, is made challenging by the stochastic nature of URLLC data packet generation. A promising solution is the adoption of predictors of URLLC data packet generation. Concretely, with reference to Fig. 1, a base station can deploy a predictor of URLLC data packet generation for the following frame, so as to guide the adaptive allocation of slots for URLLC packets, leaving the other slots available for eMBB users.

Background

URLLC traffic

A URLLC traffic must hold two restrictions:

1. Ultra-Reliability – a portion of at least 1-α of all generated packets must be scheduled for transmission.
2. Low-Latency – Each packet should have a unique schedule resource, no later than a predefined acceptable latency.

Fig 1 (a) URLLC traffic ground true generation patterns; (b) using a predictor that underestimates the traffic dynamics leads to unreliable URLLC allocation. CP-based is able to compensate successfully; (c) using a predictor that overestimates the traffic dynamics leads to overreliable URLLC allocation, i.e., low eMBB efficiency. CP-based is able to compensate successfully this as well. 

Online Conformal Prediction

CP is a class of post-hoc calibration methods that transform standard probabilistic model into a set predictor that is guaranteed to contain the true target with probability no smaller than a predetermined coverage level [1]. Online CP alleviates the limitation of conventional CP of requiring a separate calibration data at the cost of providing time-averaged, rather than ensemble, reliability guarantees [2,3]. The adoption of CP in communication engineering was proposed in [Cohen2023ICASSP], which focused on wireless applications such as symbol demodulation, modulation classification, and received signal strength prediction.

Guaranteed Dynamic Scheduling

In our new work [4], accepted at IEEE Signal Processing Letters, we introduce a novel scheduler for URLLC packets that provides formal guarantees on reliability and latency irrespective of the quality of the URLLC traffic predictor.

Fig. 2(a) illustrates the frame-based segmentation. Fig. 2(b) shows 4 URLLC generated packets and 6 pre-emptively allocated URLLC resources, yet the latest packet is not allocated a resource within the allowed latency. In contrast, Fig. 2(c) show an allocation that meets the constraints, even though the number of URLLC resources are smaller. This leaves a better portion for eMBB traffic.

Fig. 2 (a) Frame-based timelinel; (b) miscovered allocation; (c) well-covered allocation.

The proposed method leverages recent advances in online CP, and follows the principle of dynamically adjusting the amount of allocated resources so as to meet reliability and latency requirements set by the designer. To this end, we adjust a threshold that changes between frames on the basis of a reliability condition, that controls how conservative the predictor of the next frame is.

Experiments

We consider two mismatched predictors: the first underestimates the dynamic of changes the URLLC traffic, while the second overestimates.

Fig. 3 investigates of the impact of such mismatches between URLLC model parameter and ground-truth model parameter. For some parameters values of mismatch, the conventional scheduler does not hold reliability to the desired level, while for the other it may result in over reliability. The conventional scheduler is significantly affected by a mismatch between predictor and ground-truth packet generation mechanism, yielding either ill empirical coverage (below 1-α) or over coverage. In contrast, the CP-based predictor is able to flatten the coverage to asymptotically reach the long-term target 1-α.

.

Fig. 3 Empirical URLLC reliability rate and eMBB efficiency. CP-based scheduler flattens out the coverage

Full details can be found at this SPL preprint [4].

[1] Vovk, Vladimir, Alexander Gammerman, and Glenn Shafer. “Algorithmic learning in a random world,” Vol. 29. New York: Springer, 2005.

[2] Gibbs, Isaac, and Emmanuel Candes. “Adaptive conformal inference under distribution shift.” Advances in Neural Information Processing Systems 34 (2021): 1660-1672.

[3] Feldman, Shai, Stephen Bates, and Yaniv Romano. “Conformalized Online Learning: Online Calibration Without a Holdout Set.” arXiv preprint arXiv:2205.09095 (2022).

[4] Cohen, Kfir M., Sangwoo Park, Osvaldo Simeone, Petar Popovski, and Shlomo Shamai. “Guaranteed Dynamic Scheduling of Ultra-Reliable Low-Latency Traffic via Conformal Prediction.” To appear in Signal Processing Letters, [online] arXiv preprint arXiv:2302.07675 (2023).

Motivation

Artificial intelligence (AI) models typically report a confidence measure associated with each prediction, which reflects the model’s self evaluation of the accuracy of a decision. Notably, neural networks implement probabilistic predictors that produce a probability distribution across all possible values of the output variable. As an example, Fig. 1 illustrates the operation of a neural network-based demodulator, which outputs a probability distribution on the constellation points given the corresponding received baseband sample. The self-reported model confidence, however, may not be a reliable measure of the true, unknown, accuracy of the prediction, in which case we say that the AI model is poorly calibrated. Poor calibration may be a substantial problem when AI-based decisions are processed within a larger system such as a communication network.

Fig. 1 Accuracy and calibration are different properties of probabilistic predictiors.

Set Predictors

A set predictor is defined as a set-valued function that maps an input to a subset of the output domain based on a data set. As illustrated in the example of Fig. 1, it depends in general on an input, and can be taken as a measure of the uncertainty of the predictor. The performance of a set predictor is evaluated in terms of coverage and inefficiency. Coverage refers to the probability that the true label is included in the predicted set; while inefficiency refers to the average size of the predicted set. There is a clear a trade-off between two metrics.

Given a probabilistic predictor, one can construct a set predictor by relying on the confidence levels reported by the model. To this end, one can construct the smallest subset of the output domain that covers a fraction 1 − α of the probability designed by the trained model given an input. For poorly calibrated predictors, this approach cannot satisfy the coverage condition for the given desired miscoverage level α.

Conformal Prediction

In our new work [3], presented at ICASSP2023, we applied three different conformal prediction schemes for a demodulation problem:

1. Validation-based (VB) [1] – which partitions the available data set into training and validation sets. Uses the first set to train a model, and the second for calibration purpose.
2. Cross-Validation-based (CV) [2] – which trains multiple models, each using all the available data set excluding one data point, that acts as a validation example. While increasing computational complexity, in general it reduces the inefficiency of the predictive sets.
3. K-fold CV-based (K-CV) [2] – which cross-validates using a fold rather than a single point. K different models are trained using a leave-fold-out approach. This is a generalization of CV-CP set predictors that strike a balance between complexity and inefficiency by reducing the total number of model training phases to K.

Experiments

Fig. 2 shows the empirical coverage level and Fig. 3 shows the empirical inefficiency as a function of the size N of the available data set D. From Fig. 2, we first observe that the naïve set predictor, with both frequentist and Bayesian learning, does not meet the desired coverage level in the regime of a small number N of available samples. In contrast, all CP methods provide coverage guarantees, achieving coverage rates at least 1 − α. From Fig. 3, we observe that the size of the predicted sets, and hence the inefficiency, decreases as the data set size increases. Furthermore, due to their efficient use of the available data, CV and K-CV predictors have a lower inefficiency as compared to VB predictors. Finally, Bayesian NC scores are generally seen to yield set predictors with lower inefficiency, confirming the merits of Bayesian learning in terms of calibration.

Overall, the experiments confirm that all the CP-based predictors are all well-calibrated with small average set prediction size, unlike naïve set predictors that built directly on the self-reported confidence levels of conventional probabilistic predictors.

Fig. 2 Empirical coverage as function of data set size

Fig. 3 Empirical inefficiency as function of data set size

Please see preprint of the ICASSP23 paper for full details.

[1] Vovk, Vladimir, Alexander Gammerman, and Glenn Shafer. “Algorithmic learning in a random world,” Vol. 29. New York: Springer, 2005.

[2] Barber, Rina Foygel, Emmanuel J. Candes, Aaditya Ramdas, and Ryan J. Tibshirani. “Predictive inference with the jackknife+.” (2021): 486-507.

[3] Cohen, Kfir M., Park, Sangwoo,  Simeone, Osvlado, and Shamai, Shlomo (Shitz). “Calibrating AI Models for Wireless Communications via Conformal Prediction,” to appear in ICASSP 2023 [Online]. Available: https://arxiv.org/abs/2212.07775

Integrated sensing and communications (ISAC), a key enabling technology for 6G systems, leverages shared radio resources and hardware to realize the functions of sensing and communication. As an example of an application that can benefit from ISAC, consider the inter-vehicle communication scenario in Fig. 1. In it, a car wishes to send a message to a second car, while also enabling the latter to detect the presence of a possible target, e.g., of a pedestrian. While conventional systems would use two separate radio resources for data transmission and radar detection, ISAC solutions reuse the same transmitted waveform for the dual role of carrier of digital information and radar signal [1]. A natural radio interface to serve this dual function is impulse radio (IR), also known as ultrawideband (UWB). In fact, IR encodes information in the timing of pulses, which can in turn be repurposed for radar detection [2].

Fig. 1. Illustration of a neuromorphic ISAC system, in which the same IR (or UWB) signal is used for transmission and radar detection of the presence of a target. The key novel element is the use of neuromorphic computing at the ISAC receiver to simultaneously demodulate digital data and provide an online estimate of the presence or absence of the radar target.

Neuromorphic sensing and computing are emerging as alternative, brain-inspired, paradigms for efficient data collection and semantic signal processing [3]. The main features of this technology are energy efficiency, native event-driven processing of time-varying semantic sources, spike-based computing, and always-on on-hardware adaptation [4]. Neuromorphic processors, also known as spiking neural networks (SNNs), are networks of dynamic spiking neurons that mimic the operation of biological neurons. When implemented on specialized — digital or mixed analog-digital — hardware or on tailored FPGA configurations, SNNs have minimal idle and operating energy cost, and consume as little as a few picojoules per spike [5].

The integration of IR and neuromorphic computing was investigated in our recent works [6, 7], which proposed an end-to-end neuromorphic architecture for remote inference that replaces traditional digital blocks with SNNs as encoder and decoder.

Our work

With the aim of reducing energy consumption and facilitating online and always-on operation on specialized hardware, as illustrated in Fig. 1, we propose to leverage the synergy between IR transmission and neuromorphic computing to realize efficient ISAC systems. The neuromorphic ISAC (N-ISAC) receiver is able to leverage spiking neural network (SNN)-based processing to demodulate digital information and detect the radar signal.

As illustrated in Fig. 2, we consider an ISAC system in which digital communication and radar sensing leverage the same IR transmitted signal. In order to efficiently and simultaneously decode the digital data and detect the possible presence of a target at a known delay cell, the receiver processes the received signal via an SNN. Technical details can be found in our paper at this link.

Fig. 2. N-ISAC: Digital data is transmitted by an IR transmitter via pulse-position modulation (PPM); while the receiver simultaneously decodes digital data, and performs radar detection by means of an SNN, which can be efficiently implemented on neuromorphic hardware.

Result

We compare the proposed N-ISAC system with a conventional separate sensing and communications (SSAC) scheme, which divides the transmission slots into slots used for transmission and slots used for sensing. For SSAC, two SNNs are implemented at the receiver, one performing data decoding for the transmission slots, and the other responsible for radar sensing in the sensing slots.

To evaluate the performance of our system, we adopt the following performance metrics for data transmission and radar sensing: 1) Normalized test throughput, i.e., the ratio of the average number of correctly decoded bits over the total number of time slots; 2) Radar test detection error, i.e., the probability that the sensing decision is not correctly taken upon processing all time slots.

In Fig. 3, we demonstrate the normalized test throughput versus the radar test detection error for ISAC and SSAC. For the ISAC scheme, we vary a hyperparameter β dictating the relative weight in the design criterion in favor of communications; for SSAC we vary the fraction α of slots allocated to communications. As β increases, more priority is given by ISAC to communication over radar detection; and, similarly, as α increases, SSAC assigns more slots to communications. The performance of ISAC with an SNN having 10 hidden neurons is essentially independent of β for any 0.25< β <0.75. A first observation is that, for SSAC, there is a trade-off between communication and sensing performance levels caused by the slot allocation. A similar trade-off is also observed for ISAC when using an SNN with 6 hidden neurons. This is due to the limited capacity of the shared common hidden layer of the SNN. In contrast, when 10 hidden neurons are available at the SNN, ISAC is seen to optimize both data decoding and target sensing performance, obtaining significant gains over SSAC.

Fig. 3. Normalized test throughput versus radar test detection error for ISAC and SSAC.

Fig. 4 illustrates how the SNN receiver can leverage the temporal sparsity of the IR signals to enhance energy efficiency. In this regard, we recall that energy consumption in an SNN is essentially proportional to the number of spikes produced by the SNN, given extremely low idle energy of neuromorphic chips [8]. The top panel shows the transmitted IR signal consisting of two frames of transmitted signals, separated by an idle frame of duration of 20 slots. We observe that in the idle frame, the spike count is significantly reduced, showing that the neuromorphic receiver can adjust its energy consumption to the activity level of the transmitter.

Fig. 4. Top: Transmitted signal consisting of two frames in which the transmitter is active separated by an idle frame. Bottom: Corresponding spike count for the SNN.

References

[1] S. Jeong, O. Simeone, A. Haimovich, and J. Kang, “Beamforming design for joint localization and data transmission in distributed antenna system,” IEEE Transactions on Vehicular Technology, vol. 64, no. 1, pp. 62–76, 2014.

[2] A. Nezirovic, A. G. Yarovoy, and L. P. Ligthart, “Signal processing for improved detection of trapped victims using UWB radar,” IEEE Transactions on Geoscience and Remote Sensing, vol. 48, no. 4, pp. 2005–2014, 2009.

[3] A. Mehonic and A. J. Kenyon, “Brain-inspired computing needs a master plan,” Nature, vol. 604, no. 7905, pp. 255–260, 2022.

[4] M . Davies, A. Wild, G. Orchard, Y. Sandamirskaya, G. A. F. Guerra, P. Joshi, P. Plank, and S. R. Risbud, “Advancing neuromorphic computing with Loihi: a survey of results and outlook,” Proceedings of the IEEE, vol. 109, no. 5, pp. 911–934, 2021.

[5] B. Rajendran, A. Sebastian, M. Schmuker, N. Srinivasa, and E. Eleftheriou, “Low-power neuromorphic hardware for signal processing applications: a review of architectural and system-level design approaches,” IEEE Signal Processing Magazine, vol. 36, no. 6, pp. 97–110, 2019.

[6] N. Skatchkovsky, H. Jang, and O. Simeone, “End-to-end learning of neuromorphic wireless systems for low-power edge artificial intelligence,” in Proc. Asilomar Conference on Signals, Systems, and Computers, pp. 166–173, 2020.

[7] J. Chen, N. Skatchkovsky, and O. Simeone, “Neuromorphic wireless cognition: event-driven semantic communications for remote inference,” arXiv preprint arXiv:2206.06047, 2022.

[8] M . Davies, N. Srinivasa, T.-H. Lin, G. Chinya, Y. Cao, S. H. Choday, G. Dimou, P. Joshi, N. Imam, S. Jain et al., “Loihi: A neuromorphic manycore processor with on-chip learning,” IEEE Micro, vol. 38, no. 1, pp. 82–99, 2018.