The overall predictive uncertainty of a trained predictor comprises of two main contributions: the aleatoric uncertainty arising due to inherent randomness in the data generation process and the epistemic uncertainty resulting due to limitations of available training data. While the epistemic uncertainty, also called minimum excess risk, can be made to vanish with increasing training data, the aleatoric uncertainty is independent of the data. In our recent work accepted to AISTATS 2022, we provide an information-theoretic quantification of the epistemic uncertainty arising in the broad framework of Bayesian meta-learning.

Problem Formulation

In conventional Bayesian learning, the model parameter   that describes the data generating distribution is assumed to be random and is endowed with a prior distribution. This distribution is conventionally chosen based on prior knowledge about the problem. In contrast,  Bayesian meta-learning (see Fig. 1 below) aims to automatically infer this prior distribution by observing data from several related tasks. The statistical relationship among the tasks is accounted for via a global latent hyperparameter .  Specifically, the model parameter for each observed task  is drawn according to a shared prior distribution   with shared global hyperparameter . Following the Bayesian formalism, the hyperparameter is assumed to be random and distributed according to a hyper-prior distribution .

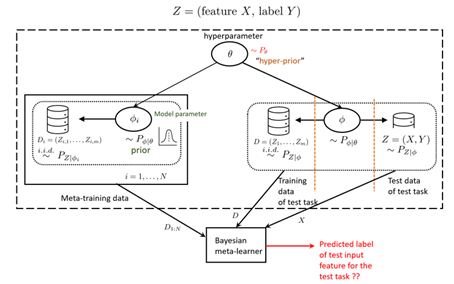
Figure 1: Bayesian meta-learning decision problem

The data from the observed related tasks, collectively called meta-training data, is used to reduce the expected loss incurred on a test task. The test task is modelled as generated by an independent model parameter  with the same shared hyperparameter. This model parameter underlies the generation of a test task training data, used to infer the task-specific model parameter, as well as a test data sample from the test task. The Bayesian meta-learning decision problem is to predict the label corresponding to test input feature of the test task, after observing the meta-training data and the training data of the test task.

A meta-learning decision rule    thus maps the meta-training data, the test task training data and test input feature to an action space.  The Bayesian meta-risk can be defined as the minimum expected loss incurred over all meta-learning decision rules, i.e., .  In the genie-aided case when the model parameter and hyper-parameter are known, the genie-aided Bayesian risk is defined as  . The epistemic uncertainty, or minimum excess risk, corresponds to the difference between the Bayesian meta-risk and Genie-aided meta-risk as  .

Main Result

Our main result shows that under the log-loss, the minimum excess meta-risk can be exactly characterized using the conditional mutual information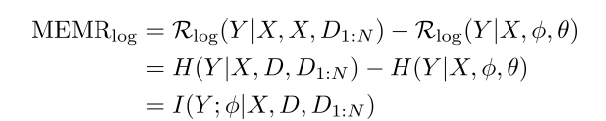

where H(A|B)  denotes the conditional entropy of A given B and  I(A;B|C) denotes the conditional mutual information between A and B given C.  This in turn implies that

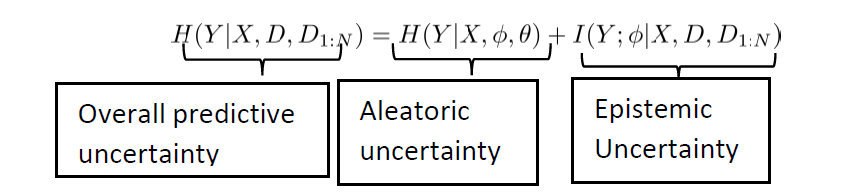
More importantly, we show that the epistemic uncertainty is contributed by two levels of uncertainties – model parameter level and hyperparameter level as

which scales in the order of 1/Nm+1/m, and vanishes as both the number of observed tasks and per-task data samples go to infinity. The behavior of the bounds is illustrated for the problem of meta-learning the Bayesian neural network prior for regression tasks in the figure below.

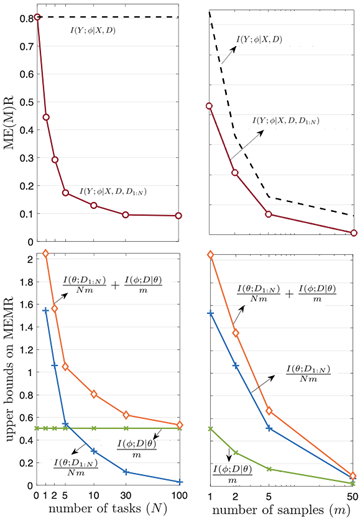
Figure 2: Performance of MEMR and derived upper bounds as a function of number of tasks and per-task data samples