In 1959 Richard Feynman gave an after-dinner talk at an American Physics Society meeting in Pasadena entitled “There’s Plenty of Room at the Bottom”,  crediting Edward Fredkin for inspiration.  In his talk, the transcription of which would later become a landmark paper in quantum computation and simulation [1], he takes some existing ideas — computation is a physical process, perhaps even a quantum mechanical one — and makes a particularly famous statement:

”I’m not happy with all the analyses that go with just classical theory, because Nature isn’t classical, dammit, and if you want to make a simulation of Nature, you’d better make it quantum mechanical, and by golly it’s a wonderful problem!”

But how can we simulate the quantum mechanical nature of Nature? This new kind of machine would become the quantum computer, and from then on, quantum computing has been on a journey with many ups and downs. Nowadays, excitement seems to be in the air again as quantum machine learning, a hybrid research discipline that combines machine learning and quantum computing, has emerged as a potential practical use of quantum hardware. Generally, quantum machine learning methods apply classical optimization routines to select parameters that define the operation of a quantum circuit. Alternative approaches, which may be more promising in the short term, involve hybrid quantum-classical models, where classical computation, e.g., for feature extraction, is combined with quantum parametric circuits [2].

Our Work

In our latest work, published in the IEEE Signal Processing Letters, we focus on the hybrid classical-quantum two-layer architecture illustrated in Fig. 1.

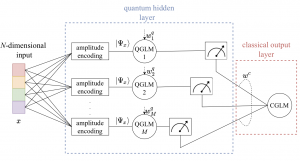
Fig. 1. In the studied hybrid classical-quantum classifier, a quantum hidden layer, fed via amplitude encoding and consisting of quantum generalized linear models (QGLMs), is followed by a classical combining output layer with a single classical GLM (CGLM) neuron. All weights and activations are binary.

In it, a first layer of quantum generalized linear models (QGLMs) is followed by a second classical combining layer. The input to the first, hidden, layer is obtained via amplitude encoding (see, e.g., [3]). Several implementations of QGLM neurons have been proposed in the literature using different quantum circuits. Given a binary input sample  and an N-dimensional vector of binary weights, the main goal of these circuits is to produce a stochastic binary output with probabilities which are a function of the inner product

between the input state and the amplitude-encoded binary weight vector

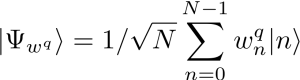
Different solutions, along with the resulting QGLM neuron’s response functions are given in the paper. For this hybrid model, we introduced a stochastic variational optimization (SVO) approach [4] that enables the joint training of quantum and classical layers via stochastic gradient descent. The proposed SVO-based training strategy operates in a relaxed continuous space of variational classical parameters.

Some Results

We show the classification accuracy, which is defined as the ratio of the number of accurate predictions over the total number of predictions made by the model, in Fig. 2 as a function of the training iterations.

 

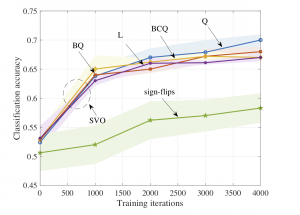
Fig. 2. Classification accuracy as a function of the training iteration for the benchmark sign-flips scheme [5] and the proposed SVO-based procedure for the BAS data set. The results are averaged over 5 independent trials.

The proposed SVO scheme is seen to achieve high classification accuracy for all of the considered response functions. In particular, the QGLM using the Quadratic (Q) response function yields fastest convergence and achieves the best performance. Due to the additional bias terms resulting from the swap test routine, the QGLMs relying on the Biased quadratic (BQ) and Biased centered quadratic (BCQ) response functions are slower to learn, but ultimately converge after around 3000 training iterations.

Please see the paper for a more extensive presentation, available here

Code, alongside a tutorial, are available here

References

[1] R. P. Feynman et al., “Simulating physics with computers,” Int. j. Theor. phys, vol. 21, no. 6/7, 1982.
[2] A. Mari, T. R. Bromley, J. Izaac, M. Schuld, and N. Killoran, “Transfer learning in hybrid classical-quantum neural networks,” Quantum, vol. 4, p. 340, 2020.
[3] M. Schuld and F. Petruccione, Machine Learning with Quantum Computers. Springer, 2021.
[4] T. Bird, J. Kunze, and D. Barber, “Stochastic variational optimization,” arXiv preprint arXiv:1809.04855, 2018.
[5] F. Tacchino, C. Macchiavello, D. Gerace, and D. Bajoni, “An artificial neuron implemented on an actual quantum processor,” npj Quantum Information, vol. 5, no. 1, pp. 1–8, 2019