Author: Nicolas Skatchkovsky

Life-long brain-inspired learning that knows what it does not know

11/10/2022 / Nicolas Skatchkovsky / 0 Comments

An emerging research topic in artificial intelligence (AI) consists in designing systems that take inspiration from biological brains. This is notably driven by the fact that, although most AI algorithms become more and more efficient (for instance, for image generation), this comes at a cost. Indeed, with architectures constantly growing in size, training a single large neural network today consumes a prohibitive amount of energy. Despite consuming only about 12W, human brains exhibit impressive capabilities, such as life-long learning.

By taking a Bayesian perspective, we demonstrate in our latest work how biologically inspired spiking neural networks (SNNs) can exhibit learning mechanisms similar to those applied in brains, which allow them to perform continual learning. As we will see, the technique also solves a key challenge in deep learning, that is, to obtain well calibrated solutions in the face of previously unseen data.

Our work

Bayesian Learning

As seen in Fig. 1, we propose to equip each synaptic weight in the SNN with a probability distribution. The distribution captures the epistemic uncertainty induced by the lack of knowledge of the true distribution of the data. This is done by assigning probabilities to model parameters that fit equally well the data, while also being consistent with prior knowledge. As a consequence, Bayesian learning is known to produce better calibrated decisions, i.e., decisions whose associated confidence better reflects the actual accuracy of the decision.

This contrasts with frequentist learning, in which the vector of synaptic weights is optimized by minimizing a training loss. The training loss is adopted as a proxy for the population loss, i.e., for the loss averaged over the true, unknown, distribution of the data. Therefore, frequentist learning disregards the inherent uncertainty caused by the availability of limited training data, which causes the training loss to be a potentially inaccurate estimate of the population loss. As a result, frequentist learning is known to potentially yield poorly calibrated, and overconfident decisions for ANNs.

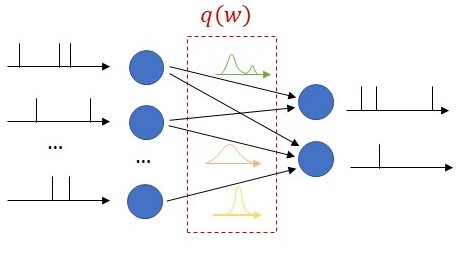
Figure 1: Illustration of Bayesian learning in an SNN: In a Bayesian SNN, the synaptic weights are assigned a joint distribution, often simplified as a product distribution across weights.

We consider both real-valued (with possibly limited resolution, as dictated by deployment on neuromorphic hardware) and binary-valued synapses, parametrised by Gaussian and Bernoulli distributions, respectively. The advantages of models with binary-valued synapses, i.e., binary SNNs, include a reduced complexity for the computation of the membrane potential. Furthermore, binary SNNs are particularly well suited for implementations on chips with nanoscale components that provide discrete conductance levels for the synapses.

Continual Learning

In addition to uncertainty quantification, we apply the proposed solution to continual learning, as illustrated in Fig. 2. In continual learning, the system is sequentially presented several datasets corresponding to distinct, but related, learning tasks, where each task is selected, possibly with replacement, from a pool of tasks, and its identity is unknown to the system. Its goal is to learn to make predictions that generalize well each new task, while causing minimal loss of accuracy on previous tasks.

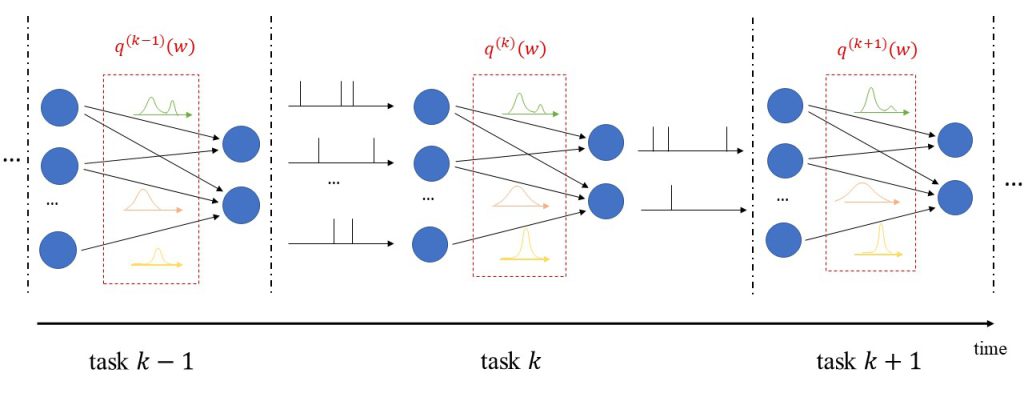
Figure 2: Illustration of Bayesian continual learning: the system is successively presented with similar, but different, tasks. Bayesian learning allows the model to retain information about previously learned information.

Many existing works on continual learning draw their inspiration from the mechanisms underlying the capability of biological brains to carry out life-long learning. Learning is believed to be achieved in biological systems by modulating the strength of synaptic links. In this process, a variety of mechanisms are at work to establish short-to intermediate-term and long-term memory for the acquisition of new information over time. These mechanisms operate at different time and spatial scales.

Biological Principles of Learning

One of the best understood mechanisms, long-term potentiation, contributes to the management of long-term memory through the consolidation of synaptic connections. Once established, these are rendered resistant to disruption by changing their capacity to change via metaplasticity. As a related mechanism, return to a base state is ensured after exposition to small, noisy changes by heterosynaptic plasticity, which plays a key role in ensuring the stability of neural systems. Neuromodulation operates at the scale of neural populations to respond to particular events registered by the brain. Finally, episodic replay plays a key role in the maintenance of long-term memory, by allowing biological brains to re-activate signals seen during previous active periods when inactive (i.e., sleeping).

In this work, we demonstrate how the continual learning rule we obtain exhibits some of these mechanisms. In particular, synaptic consolidation and metaplasticity for each synapse can be modeled by a precision parameter. A larger precision reduces the step size of the synaptic weight updates. During learning, the precision is increased to the degree that depends on the relevance of each synapse as measured by the estimated Fisher information matrix for the current mini-batch of examples.

Heterosynaptic plasticity, which drives the updates towards previously learned and resting states to prevent catastrophic forgetting, is obtained from first principles via an information risk minimization formulation with a Kullback-Leibler regularization term. This mechanism drives the updates of the precision and mean parameter towards the corresponding parameters of the variational posterior obtained at the previous task.

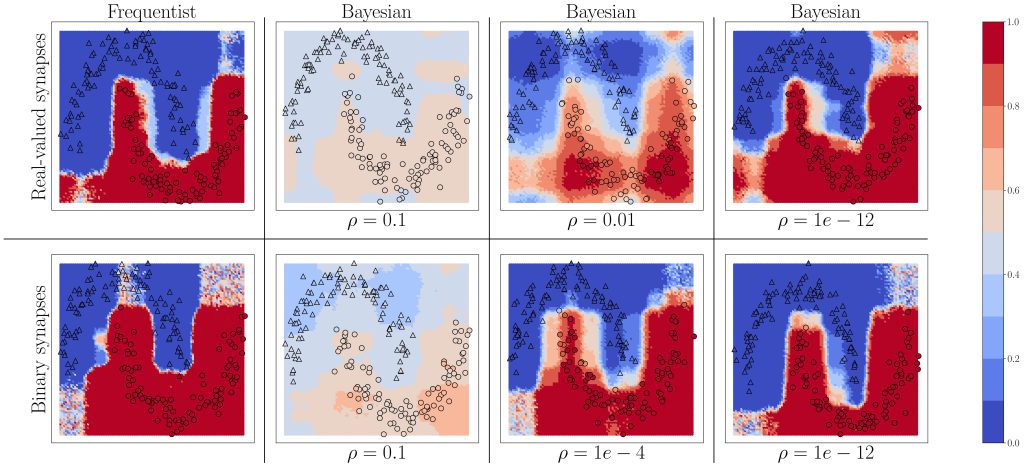
Figure 3: Predictive probabilities evaluated on the two-moons dataset after training for Bayesian learning. Top row: Real-valued synapses; Bottom row: Binary synapses.

Results

We start by considering the two-moons dataset shown in Fig. 3. Triangles indicate training points for a class “0’’, while circles indicate training points for a class “1”. The color intensity represents the predictive probabilities for frequentist learning and for Bayesian learning: the more intense the color, the higher the prediction confidence determined by the model. Bayesian learning is observed to provide better calibrated predictions, that are more uncertain outside the input regions covered by training data points. As can be seen, confidence for the Bayesian models can be mitigated by a parameter, as precised in the full text.

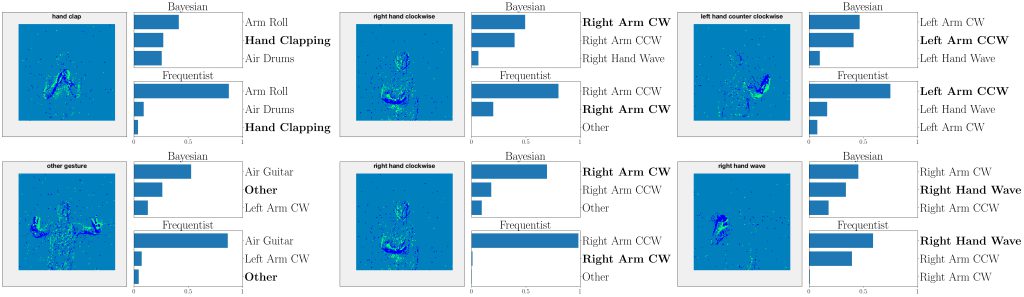
Figure 4: Top three classes predicted by both Bayesian and frequentist models on selected examples from the DVS-Gestures dataset. Top: real-valued synapses. Bottom: binary synapses. The correct class is indicated in bold font.

This point is further illustrated in Fig. 4 by showing the three largest probabilities assigned by the different models on selected examples from DVS-Gestures dataset, considering real-valued synapses in the top row and binary synapses in the bottom row. In the left column, we observe that, when both models predict the wrong class, Bayesian SNNs tend to do so with a lower level of certainty, and typically rank the correct class higher than their frequentist counterparts. Specifically, in the examples shown, Bayesian models with both real-valued and binary synapses rank the correct class second, while the frequentist models rank it third. Furthermore, as seen in the middle column, in a number of cases, the Bayesian models manage to predict the correct class, while the frequentist models predict a wrong class with high certainty. In the right column, we show that even when frequentist models predict the correct class and Bayesian models fail to do so, they still assign lower probabilities (i.e., <50%) to the predicted class.

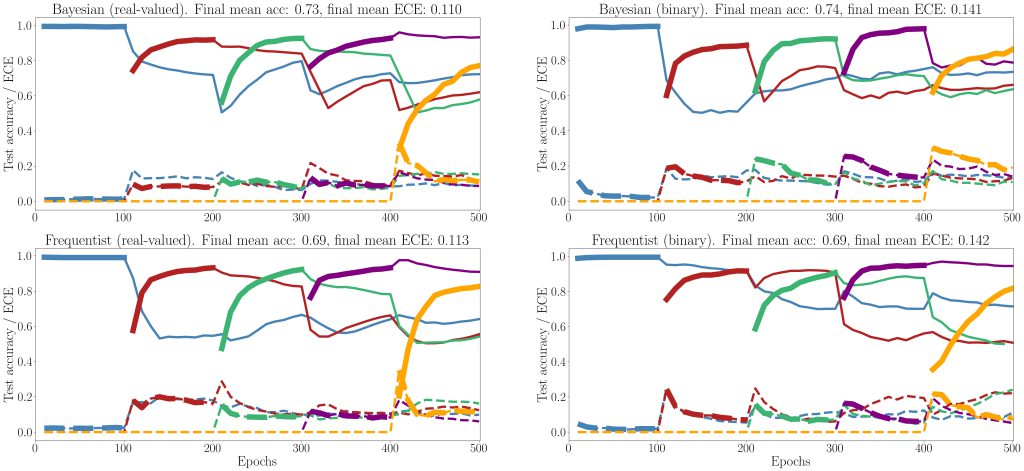
Figure 5: Evolution of the average test accuracies and ECE on all tasks of the split-MNIST-DVS across training epochs, with Gaussian and Bernoulli variational posteriors, and frequentist schemes for both real-valued and binary synapses. Continuous lines: test accuracy, dotted lines: ECE, bold: current task. Blue: {0, 1}; Red: {2, 3}; Green: {4, 5}; Purple:{6, 7}; Yellow: {8, 9}.

Finally, we show results for continual learning on the MNIST-DVS dataset in Fig. 5. We show the evolution of the test accuracy and expected calibration error (ECE) on all tasks, represented with lines of different colors, during training. The performance on the current task is shown as a thicker line. We consider frequentist and Bayesian learning, with both real-valued and binary synapses. With Bayesian learning, the test accuracy on previous tasks does not decrease excessively when learning a new task, which shows the capacity of the technique to tackle catastrophic forgetting. Also, the ECE across all tasks is seen to remain more stable for Bayesian learning as compared to the frequentist benchmarks. For both real-valued and binary synapses, the final average accuracy and ECE across all tasks show the superiority of Bayesian over frequentist learning.

More details can be found in the full text at this link.

Learning to Learn How To Spike

03/09/2021 / Nicolas Skatchkovsky / 0 Comments

Problem

Machine learning models have become a ubiquitous tool for inference in various end-user applications such as natural language processing, face recognition and mobile healthcare management. In such highly personalized cases, it is important for the model to be able to adapt to the unique features of an individual with only a minimal amount of training data. Furthermore, the devices for which these personalized inference problems are relevant are typically power and/or memory constrained which limits the size of the model that can be used for learning on the edge.

Solution

In our recent work, accepted for publication in DSLW 2021, we focus on a solution using spiking neural networks (SNNs) that leverages the popular model agnostic meta-learning method to train a model that performs online inference while concurrently improving its ability to adapt to new tasks (termed online-within-online meta-learning (OWOML)-SNN). This meta-training method learns a hyperparameter initialization that can be quickly adapted to new tasks from a certain family as opposed to the standard paradigm in which a large ‘universal’ model is fixed at deployment. Biologically inspired SNN models that operate on sparse binary signals, are known to provide benefits in terms of energy efficiency, especially (as in our case) where a local learning rule would allow it to be implemented on a neuromorphic edge processor such as Intel’s Loihi chip.

As show in Fig. 1, the proposed system assumes a stream of tasks for the SNN to adapt to, with streaming within-task data that it can learn from for online inference. Data from past tasks is stored in a fixed size buffer to be used for the meta-learning update. When new data for the current task arrives, multiple SNNs are instantiated using the hyperparameter initialization. One of those SNNs is used for online learning and inference while the others implement the meta-learning update to the hyperparameter initialization for use in the next iteration.

Results

The performance of OWOML-SNN is compared to conventional per-task training and joint training. Under conventional training, a single SNN model is randomly initialized and learns only from the data available for the current task to perform online inference. Under joint training the SNN learns a so called ‘universal’ initialization by standard training across all previous tasks and then does per-task adaptation. We consider the family of omniglot character 2-way classification tasks with rate encoding to test the within-task generalization capabilities of our meta-learner.

The results in Fig. 2 for test accuracy over training at convergence of the hyperparameter initialization and joint training initialization show that the meta-learned initialization enables the fastest online adaptation of the three, providing an improvement in accuracy over conventional training that is about 18% larger that that of joint training after training on 5 examples from each class.

Please see our paper for further details.

Bleema Rosenfeld

Sensing, Communicating, and Classifying with Spikes

09/04/2020 / Nicolas Skatchkovsky / 0 Comments

Or how to remotely classify data with 80% accuracy and zero latency at Signal-to-Noise Ratios (SNRs) as low as – 8 dB.

Problem
The development of Internet of Things (IoT) systems, with applications ranging from personal healthcare and wearable devices to drone-based monitoring, is driving research efforts on edge-based machine learning. In such systems, data may be collected by battery-powered sensors and processed at a remote device, which may itself be energy-constrained. Standard hardware implementations pose major energy and latency limitations for such applications.
In our new paper, recently accepted at Asilomar 2020, we investigate a novel solution based on neuromorphic sensors, processors, and transmitter/receivers. In neuromorphic sensors, spikes (i.e., binary signals) mark the occurrence of a relevant event, e.g., a significant change in a pixel for a neuromorphic camera. Extremely low energy is consumed when the monitored scene is idle. In neuromorphic processors, known as Spiking Neural Networks (SNNs), spiking signals are processed via dynamic neural models for the detection of spatio-temporal patterns. SNNs have recently emerged as a biologically plausible alternative to ANNs, with significant benefits in terms of energy efficiency and latency. Finally, for communications, pulses, or spikes, can encode information for radio signalling via low-power Impulse Radio (IR). Commercial products are available for all these blocks, including DVS cameras, Intel’s Loihi SNN chip, and transceivers implementing the IEEE 802.15.4z IR standard.

System model
As seen in Fig. 1, the proposed system consists of the integration of neuromorphic sensing and processing with IR transmission, and it carries out Joint Source-Channel Coding (JSCC), as it performs source and channel coding in a single step. The signal sensed by the neuromorphic sensor, e.g., a DVS camera, is encoded as a vector of binary spiking signals, and processed by an encoding SNN that performs source and channel coding. The SNN defines a probabilistic mapping that is defined by its parameter vector. The output of the encoding SNN is modulated using parallel IR transmissions, with each spike encoded by an IR waveform such as a Gaussian monopulse. The channel is modeled as a frequency-flat Gaussian channel. Finally, the received signals are classified via a decoding SNN whose output can be interpreted as a class index using standard methods for SNN-based classification. For example, rate decoding predicts a class by selecting the neurons in an output layer with the largest number of spikes.
The proposed system in Fig. 1, termed NeuroJSCC, is trained by maximizing the log-likelihood that the decoding SNN outputs desired spiking signals in response to a given input. Details on the training procedure, and the resulting algorithm, can be found in the preprint.

Experiments

To illustrate the advantage of the system, we focus on an example consisting of the remote detection of handwritten digits recorded by a neuromorphic camera.
We compare NeuroJSCC to two benchmark schemes:
1) Uncoded transmission: The observation is directly transmitted through the Gaussian channel using On-Off Shift Keying (OOK), and classified using an SNN.
2) Separate Source-Channel Coding (SSCC): The encoder applies state-of-the-art quantization based on the Vector Quantization Variational Autoencoder (VQ-VAE) scheme, followed by LDPC encoding. The spiking signal is encoded as frames, and the scheme is applied separately to each one of them. At the decoder side, frames are decoded using the Belief Propagation algorithm, decompressed using VQ-VAE decoding, and then classified. We consider two different classifiers, namely traditional ANN and SNN.
In Fig. 3, we evaluate the test accuracies at convergence obtained for different levels of SNR and the different schemes. The accuracy of Uncoded transmission drops sharply at sufficiently low SNR levels. In contrast, NeuroJSCC maintains a test accuracy of 80%, even at an SNR level as low as −8 dB. Separate SCC with an SNN as classifier suffers the most from the degradation of the SNR. Using an ANN proves more robust to low SNR levels, since an ANN can benefit from the non binary outputs of the VQ-VAE decoder without further loss of information due to binary quantization.
We refer to the main text for further experiments and analysis.
Code will be released shortly on our Github page.

Federated Neuromorphic Computing

02/21/2020 / Nicolas Skatchkovsky / 0 Comments

Problem
Training state-of-the-art Artiﬁcial Neural Network (ANN) models requires distributed computing on large mixed CPU-GPU clusters, typically over many days or weeks, at the expense of massive memory, time, and energy resources, and potentially of privacy violations. Alternative solutions for low-power machine learning on resource-constrained devices have been recently the focus of intense research. In our recently accepted paper at ICASSP 2020, we study the convergence of two such recent lines of inquiries.

On the one hand, Spiking Neural Networks (SNNs) are biologically inspired neural networks in which neurons are dynamic elements processing and communicating via sparse spiking signals over time, rather than via real numbers, enabling the native processing of time-encoded data, e.g., from DVS cameras. They can be implemented on dedicated hardware, offering energy consumptions as low as a few picojoules per spike. A more thorough introduction to probabilistic SNNs can be found in this previous blog post.

On the other hand, Federated Learning (FL) allows devices to carry out collaborative learning without exchanging local data. This makes it possible to train more effective machine learning models by beneﬁting from data at multiple devices with limited privacy concerns. FL requires devices to periodically exchange information about their local model parameters through a parameter server. It has become de-facto standard for training ANNs over large numbers of distributed devices.

System model

Figure 1 Federated Learning (FL) model under study: Mobile devices collaboratively train on-device SNNs based on different, heterogeneous, and generally unbalanced local data sets, by communicating through a base station (BS).

In our work, as seen in Figure 1, we consider a distributed edge computing architecture in which N mobile devices communicate through a Base Station (BS) in order to perform the collaborative training of local SNN models via FL. Each device holds a different local data set. The goal of FL is to train a common SNN-based model without direct exchange of the data from the local data sets.

FL proceeds in an iterative fashion across T global time-steps. To elaborate, at each global time-step, the devices refine their local model, based on their local datasets. Every τ iterations, they will also transmit their updated local model parameters to the BS, which will in turn compute a centralized averaged parameter and send it back to the devices. This global averaged parameter will be used at the beginning of the next iteration.

An SNN is a network of spiking neurons connected via an arbitrary directed graph, possibly with cycles (see Figure 2). SNNs process information through time, based on a local clock. At each local algorithmic time-step, each neuron receives the signals emitted by the subset of neurons connected to it through directed links, known as synapses. Neurons in the network will then output a binary signal, either ‘0’ or ‘1’. The instantaneous spiking probability of a neuron is determined by its past spiking behaviour and the previous spikes of its pre-synaptic neurons. SNNs are trained over sequences of S local algorithmic time-steps, made of D examples of length S’. In an image classification task, an example could be an image encoded as a binary signal.

Figure 2 Example of an internal architecture for an on-device SNN.

In FL-SNN, we cooperatively train distributed on-device SNNs thanks to Federated Learning. To that end, we derived a novel algorithm, for which the time scales involved are summarized in Figure 3. Each global algorithmic iteration t corresponds to Δs local SNN time-steps, and the total number S of SNN local algorithmic time steps and the number T of global algorithmic time steps during the training procedure are hence related as S = DS’ = T∆s.

Figure 3 Illustration of the time scales involved in the cooperative training of SNNs via FL for τ = 3 and ∆s = 4.

Experiments

We consider a classiﬁcation task based on the MNIST-DVS dataset. The training dataset is composed of 900 examples per class and the test dataset is composed of 100 samples per class. We consider 2 devices which have access to disjoint subsets of the training dataset. In order to validate the advantages of FL, we assume that the ﬁrst device has only samples from class ‘1’ and the second only from class ‘7’. We train over D = 400 randomly selected examples from the local data sets, which results in S = DS’ = 32,000 local time-steps.

As a baseline, we consider the test loss at convergence for the separate training of the two SNNs. In Figure 4, we plot the local test loss normalized by the mentioned baseline as a function of the global algorithmic time. A larger communication period τ is seen to impair the learning capabilities of the SNNs, yielding a larger ﬁnal value of the loss. In fact, for τ = 400, after a number of local iterations without communication, the individual devices are not able to make use of their data to improve performance.

Figure 4 Evolution of the mean test loss during training for different values of the communication period τ. Shaded areas represent standard deviations over 3 trials

One of the major ﬂaws of FL is the communication load incurred by the need to regularly transmit large model parameters. To partially explore this aspect, in the paper, we consider exchanging only a subset of synaptic weights during global iterations. We refer to the text at this link for details.

Integrating Wireless Access and Edge Learning

06/19/2019 / Nicolas Skatchkovsky / 0 Comments

Problem

Figure 1. Delay-constrained edge learning based on data received from a device.

The increasing number of connected devices has led to an explosion in the amounts of data being collected: smartphones, wearable devices and sensors generate data to an extent previously unseen. However, these devices often present power and computational capability constraints that do not allow them to make use of the data – for instance, to train Machine Learning (ML) models. In such circumstances, thanks to mobile edge computing, devices can rely on remote servers to perform the data processing (see Fig. 1). When the amount of data is large, or the access link slow, the amount of time required to transmit the data may be prohibitive. Given a delay constraint on the overall time available for both communication and learning, what is the joint communication-computation strategy that obtains the best performing ML model?

Pipelining communication and computation

Figure 2. Transmission and training protocol.

In a recent work to be published in IEEE Communication Letters, we propose to pipeline communication and computation with an optimized block size. We consider an Empirical Risk Minimization (ERM) problem, for which learning is carried at the server side using Stochastic Gradient Descent (SGD). As the first data block arrives at the server, training of the ML model can start. This continues by fetching data from all the data blocks received thus far. To provide some intuition on the problem of optimizing the block size, communicating the entire data set first reduces the bias of the training process but it may not leave sufficient time for learning. Conversely, transmitting very few samples in each block will bias the model towards the samples sent in the first blocks, as many computation rounds will happen based on these samples.
We determine an upper bound on the expected optimality gap at the end of the time limit, which gives us an indication on how far we are from an optimal model. We can then minimize this bound with regard to the communication block size to obtain an optimized value.

Some results

Figure 3. Training loss versus training time for different values of the block size. Solid line: experimental and theoretical optima.

Numerical experiments allowed us to compare the optimal block size found using the bound with a numerically determined optimal value found by running Monte Carlo experiments over all possible block sizes. Determining the optimal value through an extensive search over the possible block sizes allowed a gain of 3.8% in terms of the final training loss in one of our experiments (see Fig. 3). This small gain comes at the cost of a burdensome parameter optimization that took days on an HPC cluster. Minimizing the proposed bound takes seconds.
We further experimentally determined that our results, which were derived for convex loss functions satisfying the Polyak-Lojasiewicz condition, can be extended to non-convex models. As an example (not found in the paper), we studied the problem of training a multilayer perceptron with non-linear activations according to our scheme (see Fig. 4). Using the same dataset as described in the paper, we train a 2-layers perceptron with ReLU activation for the first layer and linear activation for the second. The experiments show a similar behaviour to the convex example discussed in the main text. In particular, the derived bound predicts well the existence of an optimum value of the block size (see crosses).

Figure 4. Training loss versus block size for different overhead sizes, for an MLP with non-linear activations.

The full paper can be found here.