Problem
Artificial Neural Networks (ANNs) have become the de-facto standard tool to carry out supervised, unsupervised, and reinforcement learning tasks. Their recent successes have built upon various algorithmic advances, but have also heavily relied on the unprecedented availability of computing power and memory in data centers and cloud computing platforms. The resulting considerable energy requirements run counter to the constraints imposed by implementations on low-power mobile or embedded devices for applications such as personal health monitoring or neural prosthetics.
How can the human brain perform general and complex tasks at a minute fraction of the power required by state-of-the-art supercomputers and ANN-based models? Neurons in the human brain are different from those in an ANN: they process and communicate using sparse spiking signals over time, rather than real numbers; and they are dynamic devices, rather than static non-linearites (see, Figure 1). Taking inspiration from this observation, Spiking Neural Networks (SNNs) have been introduced in the theoretical neuroscience literature as networks of dynamic spiking neurons that enables efficient on-line inference learning. SNNs have the unique capability to process information encoded in the timing of spikes, with the energy per spike being as a few picojoules. Proof-of-concept and commercial hardware implementations of SNNs (e.g., Intel, IBM) have demonstrated orders-of-magnitude improvements in terms of energy efficiency over ANNs.
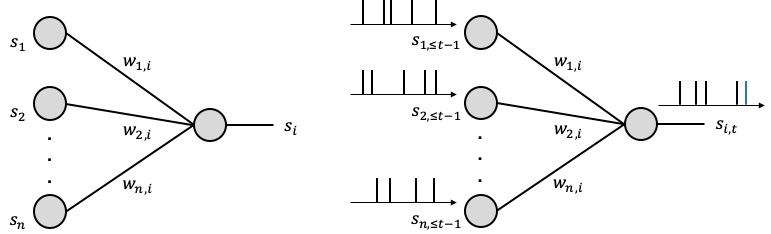
Figure 1. Illustration of neural networks: (left) an ANN, where each neuron processes real numbers; and (right) an SNN, where dynamic spiking neurons process and communicate binary sparse spiking signals over time.
The most common SNN model consists of a network of neurons with deterministic dynamics, e.g., leaky-integrate-and-fire model, whereby a spike is emitted as soon as an internal state variable, known as membrane potential, crosses a given threshold value. Learning problems should be formulated as the minimization of a loss function that directly accounts for the timing of the spikes emitted by the neurons. While this minimization can be done using Stochastic Gradient Descent (SGD) as for ANNs, it is made challenging by the non-differentiability of the behavior of spiking neurons with respect to the synaptic weights. In contrast to deterministic models, a probabilistic model for SNNs defines the outputs of all spiking neurons as differentiable joint distributed binary random processes. A probabilistic viewpoint has hence significant analytic advantages in that we can apply flexible learning rules from the principled learning criteria such as likelihood and mutual information.
Some Results
Our recent work published on IEEE Signal Processing Magazine (SPM) Special Issue on Learning Algorithms and Signal Processing for Brain-Inspired Computing provides a review on the topic of probabilistic SNNs with a specific focus on the most commonly used Generalized Linear Models (GLMs) by covering probabilistic models, learning rules, and applications.
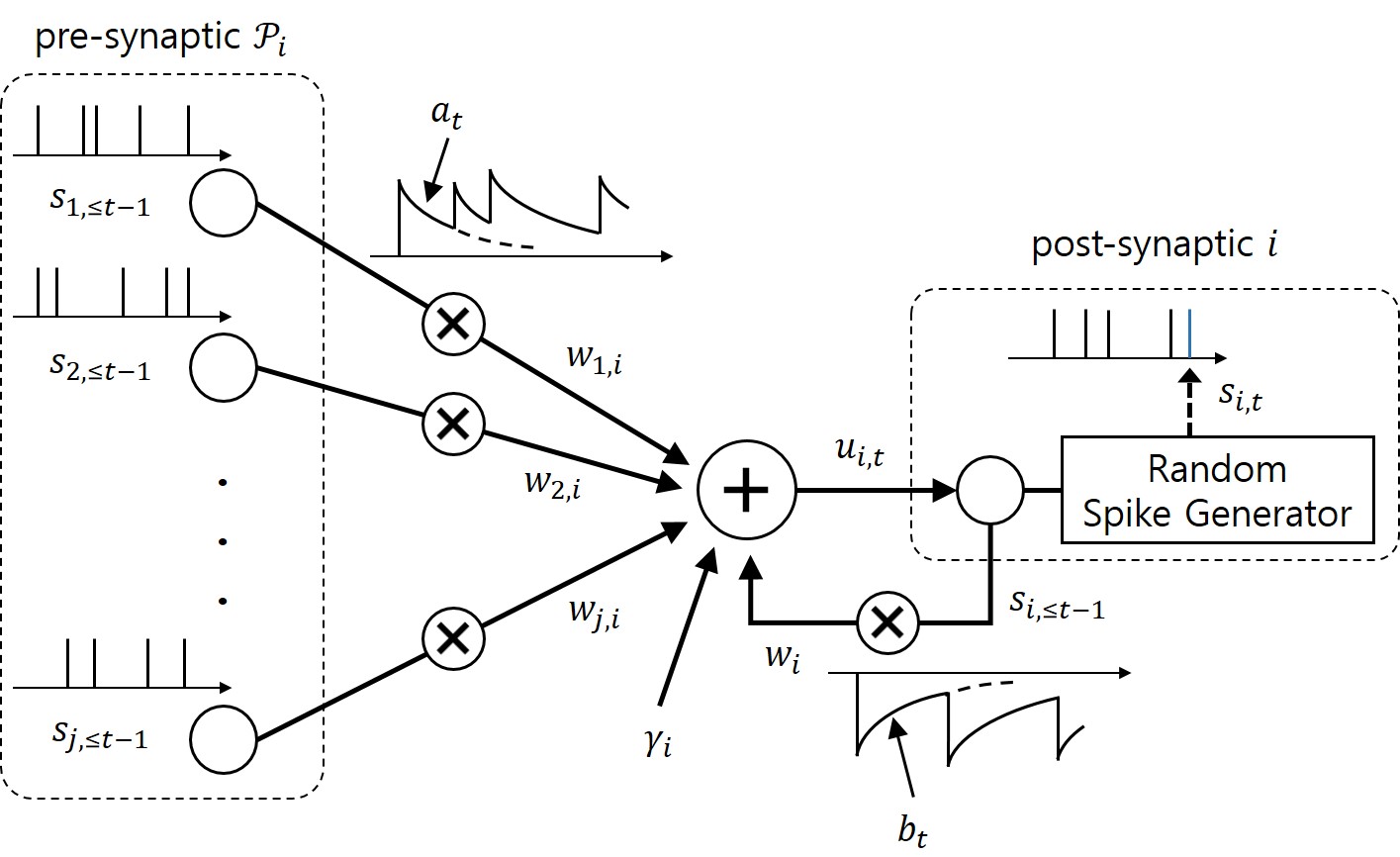
Figure 2. Illustration of the neurons with probabilistic dynamics with exponential feedforward and feedback kernels.
As illustrated in Figure 2, in a GLM, any post-synaptic neuron i receives the signals emitted by pre-synaptic neurons through synapses. Its internal state, or the probability to spike, is defined by membrane potential, which is the sum of contributions from the incoming spikes of the pre-synaptic neurons and from the past spiking behavior of the neuron itself, where both contributions are filtered by feedforward and feedback kernels, respectively. Under the GLM, the gradient of the log-likelihood of the spiking signals depends on the difference between the desired spiking behavior and its average behavior under the model.
SNNs can be trained using supervised, unsupervised, and reinforcement learning, by following a learning rule. This defines how the model parameters are updated on the basis of the available observations – in a batch mode or in an on-line fashion. Our work derives Maximum Likelihood learning rules using SGD in a batch and on-line mode, for both fully observed and partially observed SNNs. The learning rules can be interpreted in light of the general form of the three-factor rule; the synaptic weight wj,i from pre-synaptic neuron j to a post-synaptic neuron i is updated as wj,i ← wj,i + η × ℓ × pre(j) × post(i), where η is a learning rate; ℓ is a scalar global learning signal which is absent in case of fully observed SNNs; pre(j) is given by the filtered feedforward trace of the pre-synaptic neuron j; and post(i) is given by the error term of the post-synaptic neuron i, appeared in the gradient above. In case of partially observed SNNs, variational inference is needed to approximate the true posterior distribution by means of variational posterior. With a feedforward distribution for the variational posterior, we derive the learning rule using doubly SGD, whereby the global learning signal is obtained by sampling spike signals of unobserved neurons.
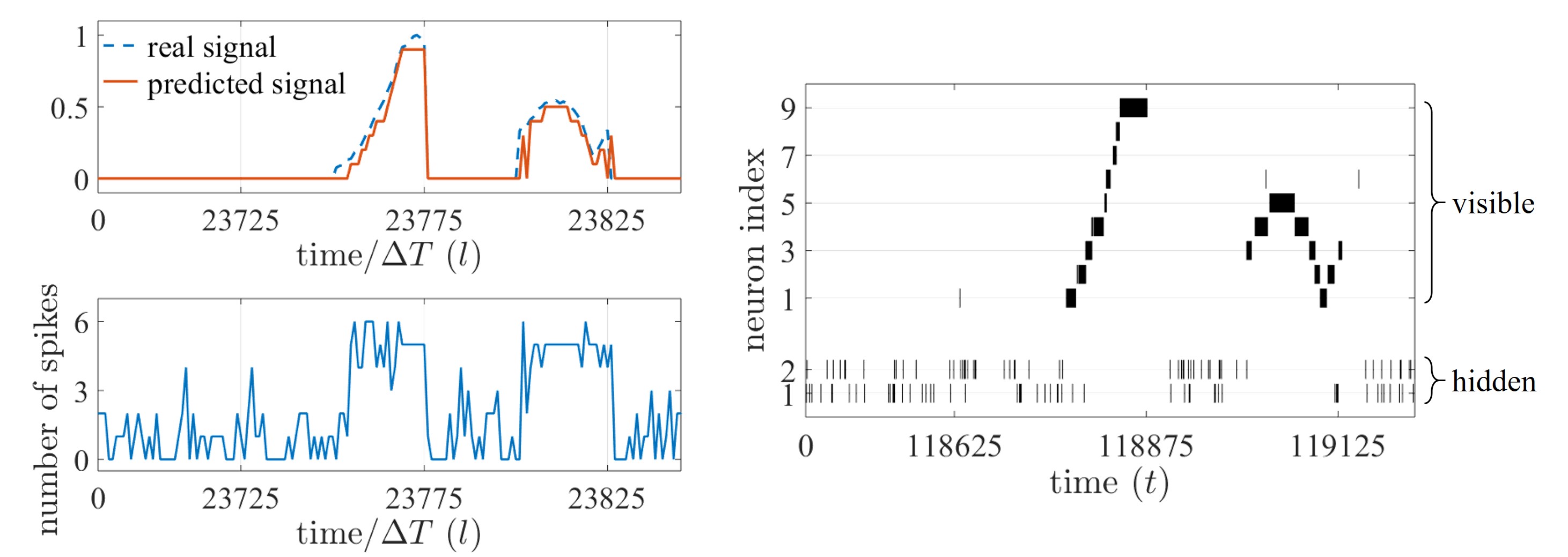
Figure 3. On-line prediction task based on an SNN with 9 visible and 2 hidden neurons; (left, top) real, analog time signal (dashed) and predicted, decoded signal (solid); (left, bottom) total number of spikes emitted by the SNN; and (right) spike raster plot of the SNN.
Experiments on an on-line prediction task allowed us to observe the potential of SNNs for ‘always-on’ event-driven applications. The SNN observes a time sequence and is trained to predict the next value of sequence given the observation of the previous values, where the time sequence is encoded in the spike domain with ΔT spike samples per each value of the sequence. In Figure 3, the SNN is seen to be able to provide an accurate prediction (left, top) with the corresponding number of spikes (left, bottom) and spikes emitted by the SNN (right). To demonstrate the efficiency benefits of SNNs that may arise from their unique time encoding capabilities, we also compare the prediction error and the number of spikes, with rate and time coding schemes.
Please refer to the full paper at IEEE Xplore (open access: arXiv) for details. The tutorial for learning algorithms and signal processing for brain-inspired computing can be found at IEEE Xplore.

Leave a Reply