Author: Matteo Zecchin

Generalization and Informativeness of Conformal Prediction

04/19/2024 / / 0 Comments

Motivation

When using a machine learning model to make important decisions, like in healthcare, finance, or engineering, we not only need accurate predictions but also want to know how sure the model is about its answers [1-3]. CP offers a practical solution for generating certified “error bars”—certified ranges of uncertainty—by post-processing the outputs of a fixed, pre-trained base predictor. This is crucial for safety and reliability. At the upcoming ISIT 2024 conference, we will present our research work, which aims to bridge the generalization properties of the base predictor with the expected size of the set predictions, also known as informativeness, produced by CP. Understanding the informativeness of CP is particularly relevant as it can usually only be assessed at test time.

Conformal prediction

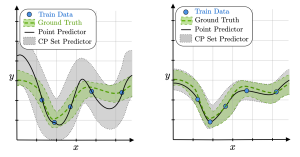
Figure 1: Conformal prediction (CP) set predictors (gray areas) obtained by calibrating a base predictor with a higher generalization error on the left and a lower generalization error on the right. Thanks to CP, both set predictors satisfy a user-defined coverage guarantee, but the inefficiency, i.e., the average prediction set size, is larger when the generalization error of the base predictor is larger.

The most practical form of CP, known as inductive CP, divides the available data into a training set and a calibration set [4]. We use the training data to train a base model, and the calibration data to determine the prediction sets around the decisions made by the base model. As shown in Figure 1, a more accurate base predictor, which generalizes better outside the training set, tends to produce more informative sets when CP is applied.

Results

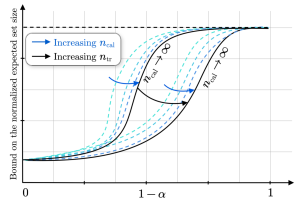
Figure 2: Bound on the average set size for different values of training and calibration data set sizes as a function of the target reliability level. Increasing the number of calibration data points causes the bound to converge exponentially fast to a function (black line) that is increasing in and decreasing in the amount of training data.

Our work’s main contribution is a high probability bound on the expected size of the predicted sets. The bound relates the informativeness of CP to the generalization properties of the base model and the amount of available training and calibration data. As illustrated in Figure 2, our bound predicts that by increasing the amount of calibration data CP’s efficiency converges rapidly to a quantity influenced by the coverage level, the size of the training set, and the predictor’s generalization performance. However, for finite amount of calibration data, the bound is also influenced by the discrepancy between the target and empirical reliability measured over the training data set. Overall, the bound justifies a common practice: allocating more data to train the base model compared to the data used to calibrate it.

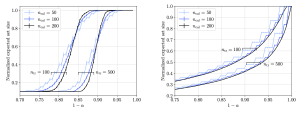
Figure 3: Normalized empirical CP set size for a multi-class classification problem on the MNIST data set as a function of the reliability level and for different sizes of the calibration and training data sets.

Since what really proves the worth of a theory is how well it holds up in real-world testing, we also compare our theoretical findings with numerical evaluations. In our study, we looked at two classification and regression tasks. We ran CP with various splits of calibration and training data, then measured the average efficiency. As shown in the Figure 3, the empirical results from our experiments matched up nicely with what our theory predicted in Figure 2.

References

[1] A. L. Beam and I. S. Kohane, “Big data and machine learning in health care,” JAMA, vol. 319, no. 13, pp. 1317–1318, 2018.

[2] J.. W. Goodell, S. Kumar, W. M. Lim, and D. Pattnaik, “Artificial intelligence and machine learning in finance: Identifying foundations, themes, and research clusters from bibliometric analysis,” Journal of Behavioral and Experimental Finance, vol. 32, p. 100577, 2021.

[3] L. Hewing, K. P. Wabersich, M. Menner, and M. N. Zeilinger, “Learning-based model predictive control: Toward safe learning in control,” Annual Review of Control, Robotics, and Autonomous Systems, vol. 3, pp. 269–296, 2020.

[4] V. Vovk, A. Gammerman, and G. Shafer, Algorithmic learning in a random world, vol. 29. Springer, 2005.

Safe Model Predictive Control via Reliable Time-Series Forecasting

12/04/2023 / / 0 Comments

Motivation

The control of dynamical systems is the backbone of modern technologies, ranging from industrial processes to autonomous vehicles. In many of these scenarios, systems must be controlled while satisfying a set of safety and reliability constraints with respect to the unknown evolution of a target process. For example, as illustrated in Figure 1, autonomous vehicles or unmanned aerial vehicles (UAVs) must plan their trajectory while maintaining a safe distance from other vehicles or obstacles. To this end, predictions about the future evolution of the system must be used. In this context, a primary challenge is to ensure safety and reliability in the face of predictions that are often uncertain.

Figure 1: UAV tracking problem, an example of model predictive control in which the UAV must plan its path based on the unknown evolution of the object to be tracked.

Probabilistic Time Series-Conformal Risk Prediction

To support the deployment of reliable control mechanisms for dynamical system, in our work we have recently proposed probabilistic time series-conformal risk prediction (PTS-CRC). PTS-CRC is a novel post-hoc calibration procedure that operates on the predictions produced by any pre-designed probabilistic forecaster to yield reliable time series prediction sets. As illustrated in Figure 2, PTS-CRC generates predictive sets based on an ensemble of multiple prototype trajectories sampled from the probabilistic model, supporting the efficient representation of forking uncertainties. This contrasts with previous solutions that apply Conformal Prediction[1] to deterministic predictors (TS-CP)[2], which are bounded to produce compact prediction sets. Furthermore, sets produced by PTS-CRC can be calibrated to satisfy a wide array of reliability definitions, beyond the standard one of coverage.

Figure 2: Construction of a prototype-based set predictor based on 3 prototypical sequences.

PTS-CRC Based Model Predictive Control

Based on the reliability properties of PTS-CRC predictions, we devise a novel Model Predictive Control (MPC) framework that addresses open-loop and closed-loop control problems under general average constraints on the quality or safety of the control policy. The key idea is to derive the control by replacing constraints that depend on the unknown dynamics of the target process with those depending on the predictive sets output by PTS-CRC. The reliability requirements of PTS-CRC predictions translate into reliability requirements for the original control problem.

Experiments

We apply PTS-CRC-based MPC to wireless networking problems, specifically focusing on a scenario where a base station must modulate its future power allocation based on the unknown evolution of channel conditions. For instance, we address the challenge of controlling transmit power to maximize the communication rate at an unlicensed user while adhering to a safety requirement, expressed as the maximum interference experienced by a licensed user. By employing PTS-CRC, we can replace the unknown system evolution with efficient multimodal predictive sets that more effectively capture multimodal channel evolution compared to TS-CP (Figure 3). As exemplified in Figure 4, PTS-CRC-based power control leads to power allocations that achieve a higher communication rate compared to TS-CP.

Figure 3: Comparison between the prediction sets of TS-CP and PTS-CRC for the problem of channel gain evolution forecasting.

Figure 4: Comparison between the power control solution obtained using PTS-CRC and TS-CP based MPC.

References

[1] Vovk, Vladimir, Alexander Gammerman, and Glenn Shafer. “Algorithmic learning in a random world,” Vol. 29. New York: Springer, 2005.

[2] Stankeviciute, Kamile, Ahmed M Alaa, and Mihaela van der Schaar. “Conformal time-series forecasting.” Advances in neural information processing systems 34, 2021.

[3] Zecchin, Matteo, Sangwoo Park, and Osvaldo Simeone. “Forking Uncertainties: Reliable Prediction and Model Predictive Control with Sequence Models via Conformal Risk Control.” arXiv preprint arXiv:2310.10299, 2023.

© 2024 King's Communications, Learning & Information Processing lab

Theme by Anders Norén — Up ↑