Author: Sangwoo Park

Wireless Reliable Federated Inference

02/08/2024 / / 0 Comments

Written by Meiyi Zhu during her visit to KCLIP.

Motivation

Consider a wireless federated inference scenario in which the devices and a server share a pre-trained machine learning model, e.g., trained via federated learning. The server wishes to make an inference on its own new input based on such a pre-trained machine learning model. Note that the server has no access to the data; the data is only presented at the devices. This scenario is common in practice. For example, a personal healthcare system would first train the respective model via federated learning, without acquiring personal data from the end users; while upon achieving a trained healthcare model, wishes to provide useful solution to new users. We will assume that new users ask queries to the central server, while the general conclusion made in this article retains even for the case in which the new user has its own access to the pre-trained model.

However, depending on the quality of the pre-trained model, e.g., lack of data, the solution provided by the pre-trained model may yield wrong decisions. More importantly, such model is likely to yield unreliable decisions; see, e.g., our previous post ‘Is Accuracy Sufficient for AI in 6G? (No, Calibration is Equally Important)’. As reliability plays an important role in various fields including healthcare monitoring and autonomous vehicle navigation, it is important to find ways to make the federated inference reliable. But how can we make the pre-trained model reliable as the central server has no access to the data at all?

Recent work has introduced federated conformal prediction (CP), which improves the reliability of the server’s decision by utilizing available held-out local data at each device, of course, without central server’s access to such data. The goal of federated CP is to provide a guaranteed interval or set of potential outputs that contains the correct answer at a predefined reliability level [1, 2]. As a state-of-the-art solution, reference [1] proposed a quantile-of-quantile (QQ) scheme, referred to as FedCP-QQ, whereby each device computes and communicates a pre-determined quantile of the local losses. However, existing work assumed noise-free communication between the server and the devices, whereby devices can communicate a single real number to the server.

Wireless Federated Conformal Prediction

In our recent work, to appear in Transactions on Signal Processing, we study for the first time federated CP in a wireless setting, as illustrated in Fig. 1. Specifically, we introduce a novel protocol, termed wireless federated conformal prediction (WFCP), which builds on type-based multiple access (TBMA) and on a novel quantile correction scheme.

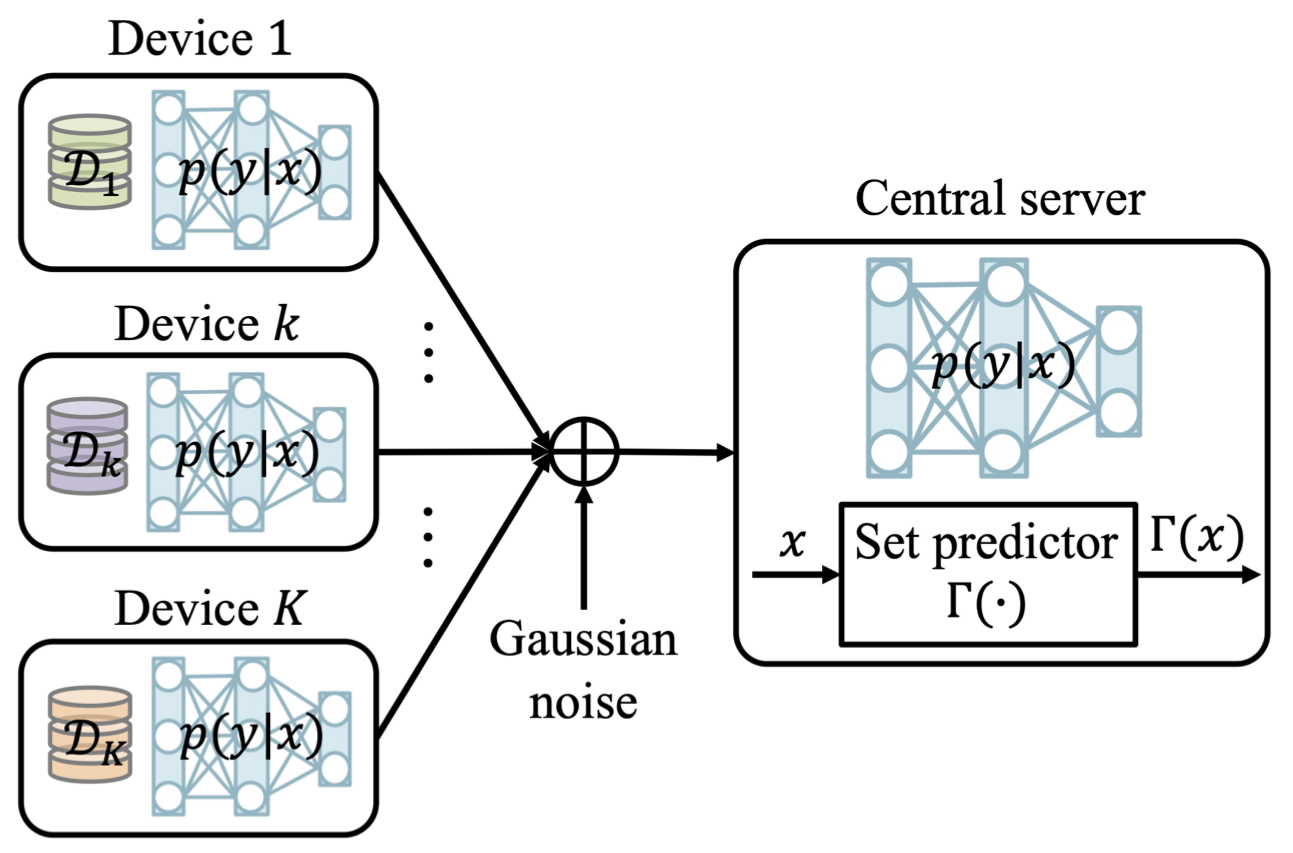
Fig. 1. Illustration of the wireless reliable federated inference problem under study.

TBMA is a multiple access scheme that aims at recovering aggregated statistics, rather than individual messages [3]. By noting that federated CP also requires aggregated statistics across the devices, i.e., quantile, we have proposed to apply TBMA for WFCP. More precisely, as illustrated in Fig. 2, TBMA enables the estimate of the global histogram of data available across all devices without having to separately estimate the histograms of all devices. Specifically, each histogram bin is assigned an orthogonal codeword and the server can estimate the global histogram thanks to the superposition property of wireless communications. In this way, WFCP enables a direct estimate of the global quantile at the server without imposing bandwidth requirements that scale linearly with the number of active devices like FedCP-QQ. Rather, the communication requirements of WFCP are only dictated by the precision with which the signals are represented for transmission to the server, i.e., the length of each codeword.

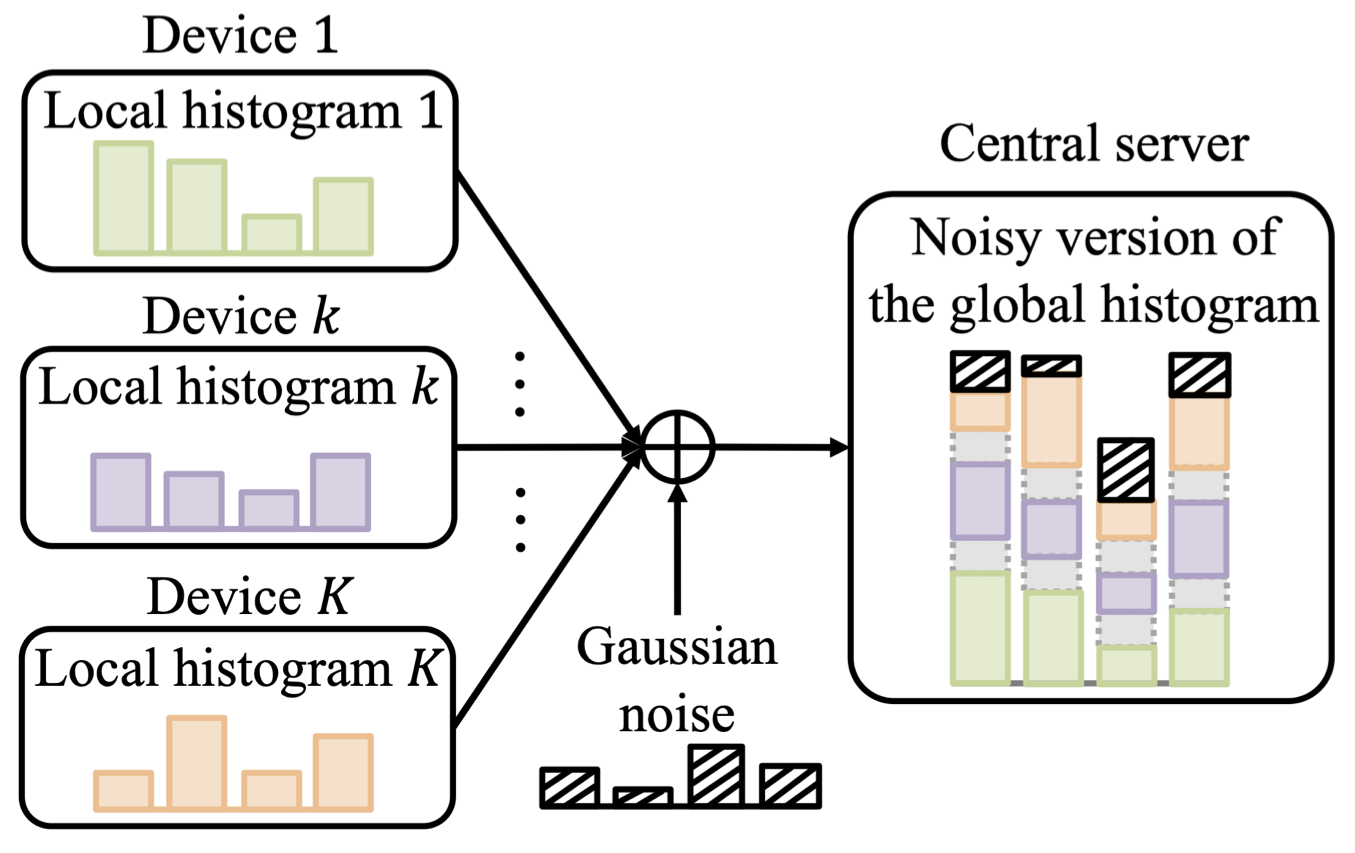
Fig. 2. Illustration of the TBMA enabled communication model.

The other key technical challenge tackled in our work is the derivation of a novel quantile correction approach that ensures the reliability of the set predictor despite the presence of channel noise.

Experiments

We evaluate our proposed WFCP on CIFAR-10 data set over Rayleigh fading channels. We show here one of the results that plots the performance gains of WFCP in the presence of limited communication resources. In Fig. 3, we evaluate the performance of WFCP and our implementation of existing FedCP-QQ (DQQ) over wireless channels using finite blocklength information theory as a function of SNR. As SNR increases, both WFCP and DQQ maintain the target reliability level, while offering a decreasing prediction set size. Across all the SNRs, WFCP generates a more informative predicted set than DQQ, and it approaches the performance of the centralized CP. Please refer to our paper for more details.

 

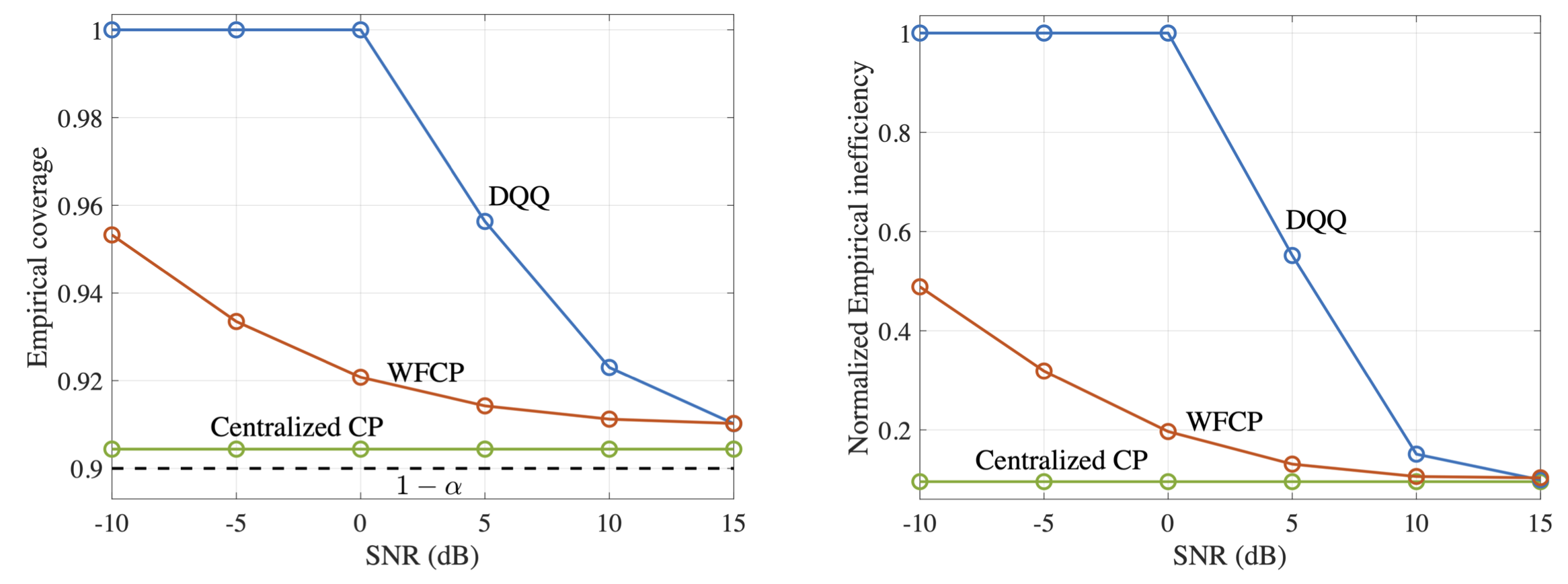
Fig. 3. Empirical coverage and normalized empirical inefficiency of centralized CP, WFCP, and digital implementation of existing FedCP-QQ [1].

References

[1] P. Humbert, B. Le Bars, A. Bellet, and S. Arlot, “One-shot federated conformal prediction,” ICML 2023

[2] C. Lu and J. Kalpathy-Cramer, “Distribution-free federated learning with conformal predictions,” arXiv:2110.07661, 2021

[3 G. Mergen and L. Tong, “Type based estimation over multiaccess channels,” IEEE TSP 2006

Learning to Learn How to Calibrate

12/08/2022 / / 0 Comments

As discussed in our previous post ‘Is Accuracy Sufficient for AI in 6G? (No, Calibration is Equally Important)’, reliable AI should be able to quantify its uncertainty, i.e., to “know when it knows” and “know when it does not know”. To obtain reliable, or well-calibrated, AI models, two types of approaches can be adopted: (i) training-based calibration, and (ii) post-hoc calibration. Training-based calibration modifies the training procedure by accounting for calibration performance, and includes methods such as Bayesian learning [1, 2], robust Bayesian learning [3, 4], and calibration-aware regularization [5]; while post-hoc calibration utilizes validation data to “recalibrate” a probabilistic model, as in temperature scaling [6], Platt scaling [7], and isotonic regression [8]. All these methods have no formal guarantees on calibration, either due to inevitable model misspecification [9], or due to overfitting to the validation set [10, 11]. In contrast, conformal prediction (CP) offers formal calibration guarantees, although calibration is defined in terms of set, rather than probabilistic, prediction [12]. 

Fig. 1. Improvements in calibration can be obtained by either (i) training-based calibration or (ii) post-hoc calibration. Only conformal prediction, a post-hoc calibration approach, provides formal guarantees on calibration via set prediction.

A well-calibrated set predictor is the one that contains the true label with probability no smaller than a predetermined coverage level, say 90%. A set predictor obtained by conformal prediction is provably well calibrated, irrespective of the unknown underlying ground-truth distribution as long as the data examples are exchangeable, or i.i.d. (independent and identically distributed). 

One could trivially build a well-calibrated set predictor by producing the entire label set as the predicted set. However, such set predictor would be completely uninformative, since the size of the set predictor determines how informative the set predictor is. While conformal prediction is always guaranteed to yield reliable set predictors, it may produce large predicted set size in the presence of limited data examples [13]. In our recent work, presented at the NeurIPS 2022 Workshop on Meta-Learning, we have introduced a novel method that enhances the informativeness of CP-based set predictors via meta-learning.

Fig. 2. Meta-learning transfers knowledge from multiple tasks. In our recent paper, we have proposed an application of meta-learning to conformal prediction with the aim of reducing the average prediction set size while preserving formal calibration guarantees.

Meta-learning, or learning to learn, transfers knowledge from multiple tasks to optimize the inductive bias (e.g., the model class) for new, related, tasks [14]. In our recent work, meta-learning was applied to cross-validation-based conformal prediction (XB-CP) [13] to achieve well-calibrated and informative set predictors. As demonstrated in the following figure, the proposed meta-learning approach for XB-CP, termed meta-XB, can reduce the average prediction set size as compared to conventional CP approaches (XB-CP and validation-based conformal prediction (VB-CP) [12]) and to previous work on meta-learning for VB-CP [14], while preserving the formal guarantees on reliability (the predetermined coverage level, 90%, is always satisfied for meta-XB). 

Fig. 3. Average prediction set size (left) and coverage (right) for new tasks as a function of number of meta-training tasks. As compared to conventional CP schemes (VB-CP and XB-CP), meta-learning based approaches (meta-VB and meta-XB) have smaller prediction set size; while the proposed meta-XB guarantees reliability for every task unlike meta-VB that satisfies coverage condition on average over multiple tasks.

For more details including improvements in terms of input-conditional coverage via meta-learning with adaptive nonconformity scores [15], and further experimental results on image classification and communication engineering aspects, please refer to the arXiv posting.

References

[1] O. Simeone, Machine learning for engineers. Cambridge University Press, 2022

[2] J. Knoblauch, et al, “Generalized variational inference: Three arguments for deriving new posteriors,” arXiv:1904.02063, 2019

[3] W. Morningstar, et al “PACm-Bayes: Narrowing the empirical risk gap in the Misspecified Bayesian Regime,” NeurIPS 2021

[4] M. Zecchin, et al, “Robust PACm: Training ensemble models under model misspecification and outliers,” arXiv:2203.01859, 2022

[5] A. Kumar, et al, “Trainable calibration measures for neural networks from kernel mean embeddings,” ICML 2018

[6] C. Guo, et al, “On calibration of modern neural networks,” ICML 2017

[7] J. Platt, et al, “Probabilistic outputs for support vector machines and comparisons to regularized likelihood method,” Advances in Large Margin Classifiers 1999

[8]  B. Zadrozny and C. Elkan “Transforming classifier scores into accurate multiclass probability estimates,” KDD 2022

[9] A. Masegosa, “Learning under model misspecification: Applications to variational and ensemble methods.” NeurIPS 2020

[10] A. Kumar, et al, “Verified Uncertainty Calibration,” NeurIPS 2019

[11] X. Ma and M. B. Blaschko, “Meta-Cal: Well-controlled Post-hoc Calibration by Ranking,” ICML 2021 

[12]  V. Vovk, et al, “Algorithmic Learning in a Random World,” Springer 2005

[13] R. F. Barber, et al, “Predictive inference with the jackknife+,” The Annals of Statistics, 2021

[14] Chen, Lisha, et al. “Learning with limited samples—Meta-learning and applications to communication systems.” arXiv preprint arXiv:2210.02515, 2022.

[14] A. Fisch, et al, “Few-shot conformal prediction with auxiliary tasks,” ICML 2021

[15] Y. Romano, et al, “Classification with valid and adaptive coverage,” NeurIPS 2020

 

Meta-learning: A new framework for few-pilot transmission in IoT networks

06/06/2019 / / 0 Comments

Problem

Fig. 1: Illustration of few-pilot training for an IoT system via meta-learning

For channels with an unknown model or an unavailable optimal receiver of manageable complexity, the design of demodulation and decoding can potentially benefit from a data-driven approach based on machine learning. Machine learning solutions, however, cannot be directly applied to Internet- of-Things (IoT) scenarios in which devices transmit sporadically using short packets with few pilot symbols. In fact, the few pilots do not provide enough data for training the receiver.

A Novel Solution based on Meta-learning

Fig. 2: MAML is to find an initial value 𝜃 that minimizes the loss L𝑘(θ´𝑘) for all devices 𝑘 after one step of update. In contrast, joint training carries out an optimization on the cumulative loss              L1(θ) + L2(θ) 

In a recent work to be presented at IEEE SPAWC 2019, we proposed a novel solution for demodulation in IoT networks that is based on model-agnostic meta-learning (MAML) algorithm. The key idea is to use pilots from previous transmissions of other IoT devices as meta- training data in order to learn a demodulator that is able to quickly adapt to the end-to-end channel conditions of a new device from few pilots. MAML derives an inductive bias as an initialization point for a neural network-based demodulator. As illustrated in Fig. 2, MAML seeks an initialization point such that all the performance losses of the demodulators for all IoT devices obtained after one update are collectively minimized. In comparison, a more conventional approach to use meta-training data, namely joint training, would pool together all the pilots received from the meta-training devices and seeks for minimizing the cumulative loss.

Some Results

To give a taste of the results in the paper, we now provide an example.

Fig. 3: Probability of symbol error with respect to number of pilots for the  meta-test device (see paper).

In Fig. 3, we plot probability of symbol error with respect to the number of pilots for new IoT device in offline scenario. We adopt 16-QAM with 100 meta-training devices, each with 32 pilots for meta-training. We compare the performance of state-of-the-art meta-learning approaches including MAML with: (i) a fixed initialization scheme where data from the meta-training devices is not used; (ii) joint training with the meta-training dataset as described above.

All of the various meta-learning schemes are seen to vastly outperform the mentioned baseline approaches (i) – (ii) by adapting to the channel of the meta-test device using only a few pilots. In contrast, joint training shows similar performance compared to fixed initialization. This confirms that, unlike conventional solutions, meta-learning can effectively transfer information from meta-training devices to a new target device.

 

Fig. 4: Average probability of symbol error with respect to average number of pilots over slots t=71, …, 90 for online meta-learning (see paper).

In Fig. 4, we plot probability of symbol error with respect to average number of pilots in online scenario. Through comparison with fixed initialization case, we have shown that proposed adaptive pilot number selection scheme can reduce pilot overhead with any online schemes. Moreover, when proposed scheme comes with online meta-learning, we show that pilot overhead is reduced even more under negligible performance degradation. This again confirms that meta-learning can acquire useful inductive bias from previous IoT devices.

The full paper can be found here.

© 2024 King's Communications, Learning & Information Processing lab

Theme by Anders Norén — Up ↑