Written by Meiyi Zhu during her visit to KCLIP.
Motivation
Consider a wireless federated inference scenario in which the devices and a server share a pre-trained machine learning model, e.g., trained via federated learning. The server wishes to make an inference on its own new input based on such a pre-trained machine learning model. Note that the server has no access to the data; the data is only presented at the devices. This scenario is common in practice. For example, a personal healthcare system would first train the respective model via federated learning, without acquiring personal data from the end users; while upon achieving a trained healthcare model, wishes to provide useful solution to new users. We will assume that new users ask queries to the central server, while the general conclusion made in this article retains even for the case in which the new user has its own access to the pre-trained model.
However, depending on the quality of the pre-trained model, e.g., lack of data, the solution provided by the pre-trained model may yield wrong decisions. More importantly, such model is likely to yield unreliable decisions; see, e.g., our previous post ‘Is Accuracy Sufficient for AI in 6G? (No, Calibration is Equally Important)’. As reliability plays an important role in various fields including healthcare monitoring and autonomous vehicle navigation, it is important to find ways to make the federated inference reliable. But how can we make the pre-trained model reliable as the central server has no access to the data at all?
Recent work has introduced federated conformal prediction (CP), which improves the reliability of the server’s decision by utilizing available held-out local data at each device, of course, without central server’s access to such data. The goal of federated CP is to provide a guaranteed interval or set of potential outputs that contains the correct answer at a predefined reliability level [1, 2]. As a state-of-the-art solution, reference [1] proposed a quantile-of-quantile (QQ) scheme, referred to as FedCP-QQ, whereby each device computes and communicates a pre-determined quantile of the local losses. However, existing work assumed noise-free communication between the server and the devices, whereby devices can communicate a single real number to the server.
Wireless Federated Conformal Prediction
In our recent work, to appear in Transactions on Signal Processing, we study for the first time federated CP in a wireless setting, as illustrated in Fig. 1. Specifically, we introduce a novel protocol, termed wireless federated conformal prediction (WFCP), which builds on type-based multiple access (TBMA) and on a novel quantile correction scheme.
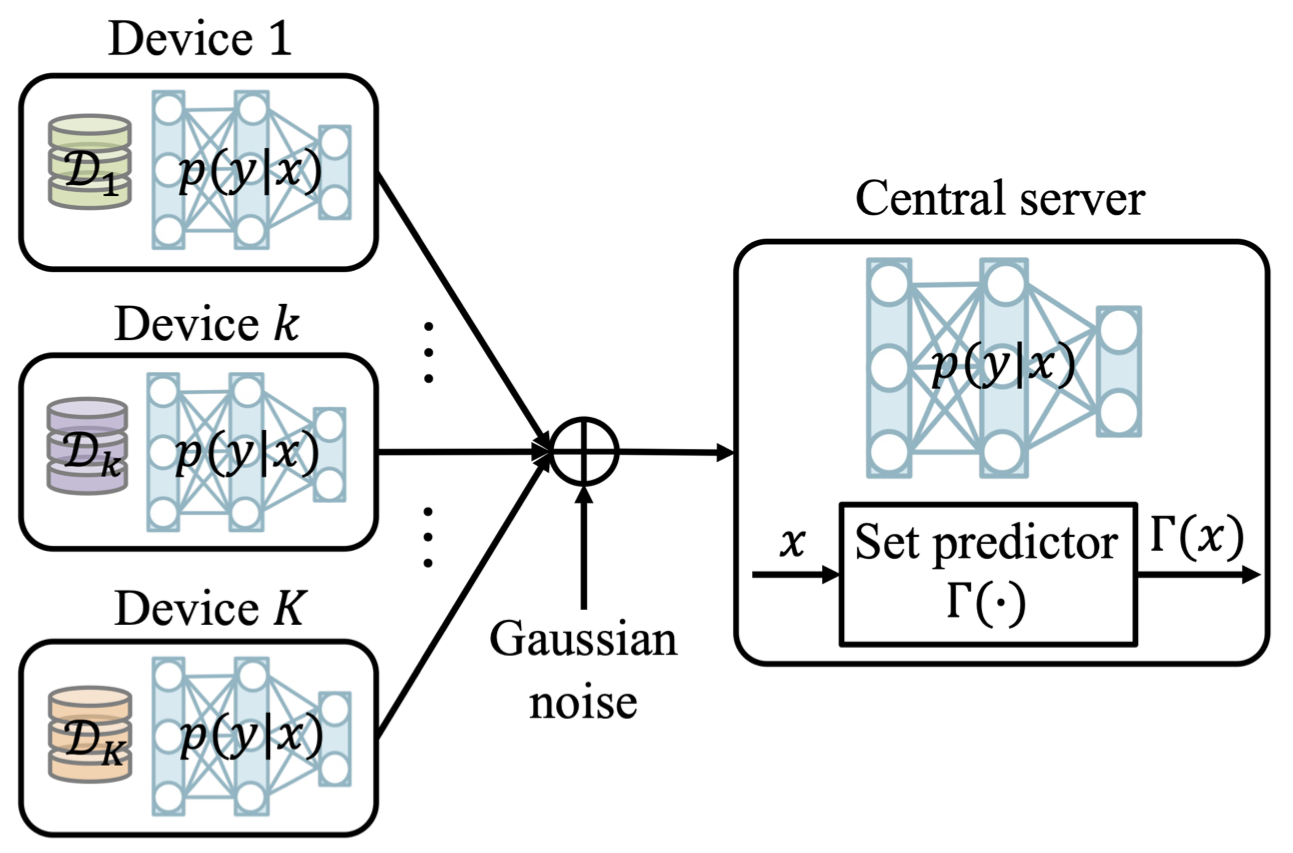
Fig. 1. Illustration of the wireless reliable federated inference problem under study.
TBMA is a multiple access scheme that aims at recovering aggregated statistics, rather than individual messages [3]. By noting that federated CP also requires aggregated statistics across the devices, i.e., quantile, we have proposed to apply TBMA for WFCP. More precisely, as illustrated in Fig. 2, TBMA enables the estimate of the global histogram of data available across all devices without having to separately estimate the histograms of all devices. Specifically, each histogram bin is assigned an orthogonal codeword and the server can estimate the global histogram thanks to the superposition property of wireless communications. In this way, WFCP enables a direct estimate of the global quantile at the server without imposing bandwidth requirements that scale linearly with the number of active devices like FedCP-QQ. Rather, the communication requirements of WFCP are only dictated by the precision with which the signals are represented for transmission to the server, i.e., the length of each codeword.
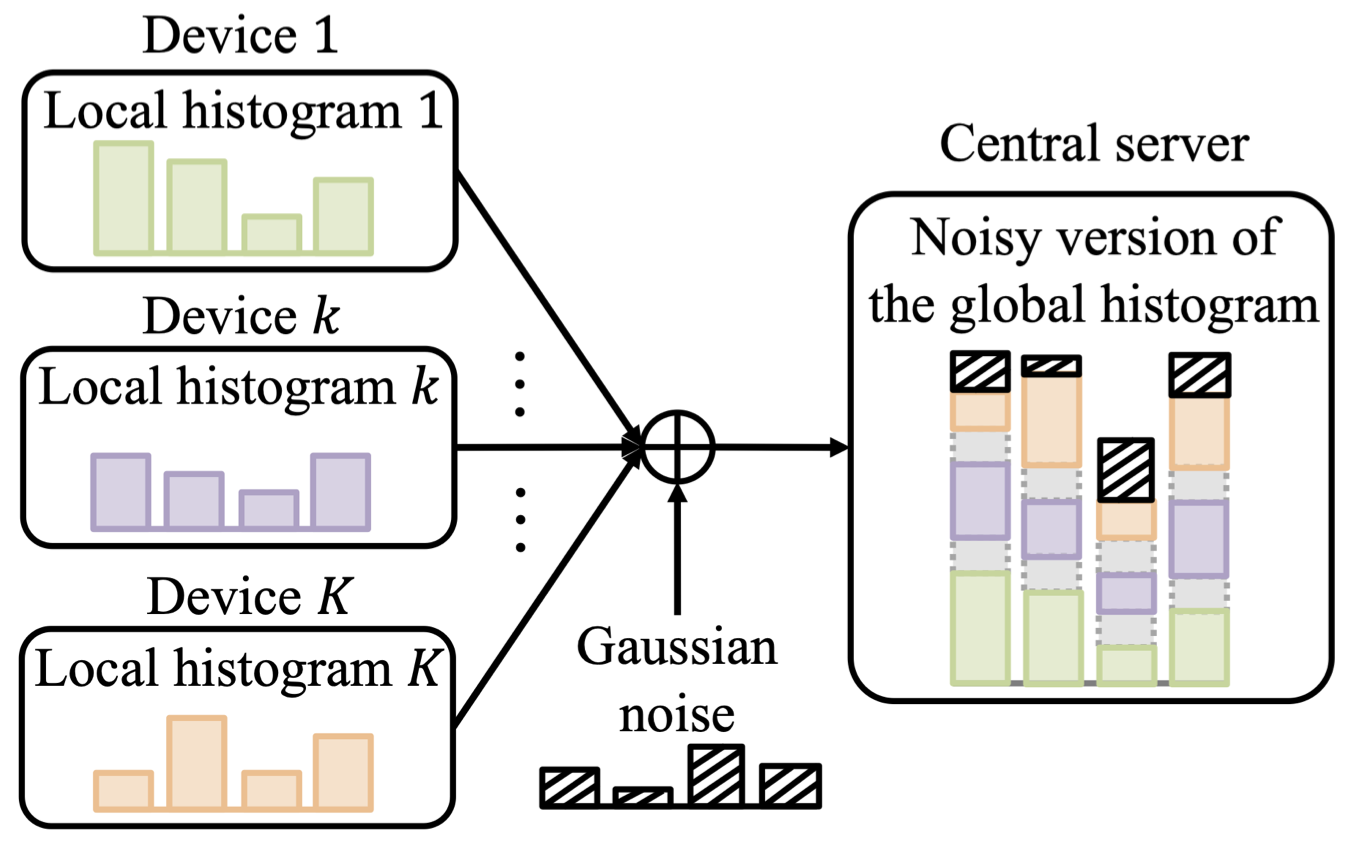
Fig. 2. Illustration of the TBMA enabled communication model.
The other key technical challenge tackled in our work is the derivation of a novel quantile correction approach that ensures the reliability of the set predictor despite the presence of channel noise.
Experiments
We evaluate our proposed WFCP on CIFAR-10 data set over Rayleigh fading channels. We show here one of the results that plots the performance gains of WFCP in the presence of limited communication resources. In Fig. 3, we evaluate the performance of WFCP and our implementation of existing FedCP-QQ (DQQ) over wireless channels using finite blocklength information theory as a function of SNR. As SNR increases, both WFCP and DQQ maintain the target reliability level, while offering a decreasing prediction set size. Across all the SNRs, WFCP generates a more informative predicted set than DQQ, and it approaches the performance of the centralized CP. Please refer to our paper for more details.
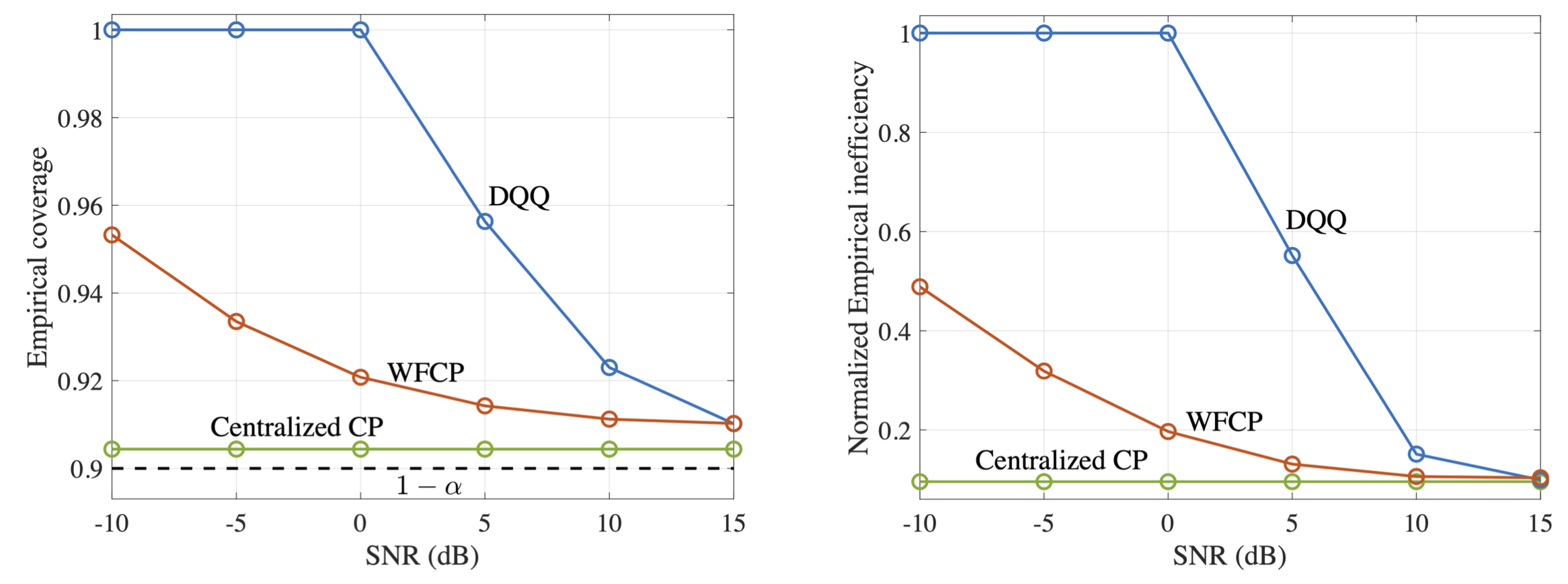
Fig. 3. Empirical coverage and normalized empirical inefficiency of centralized CP, WFCP, and digital implementation of existing FedCP-QQ [1].
References
[1] P. Humbert, B. Le Bars, A. Bellet, and S. Arlot, “One-shot federated conformal prediction,” ICML 2023
[2] C. Lu and J. Kalpathy-Cramer, “Distribution-free federated learning with conformal predictions,” arXiv:2110.07661, 2021
[3 G. Mergen and L. Tong, “Type based estimation over multiaccess channels,” IEEE TSP 2006


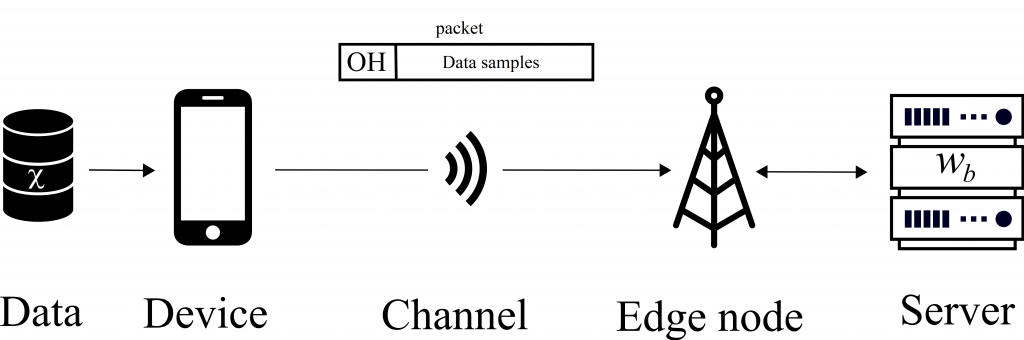
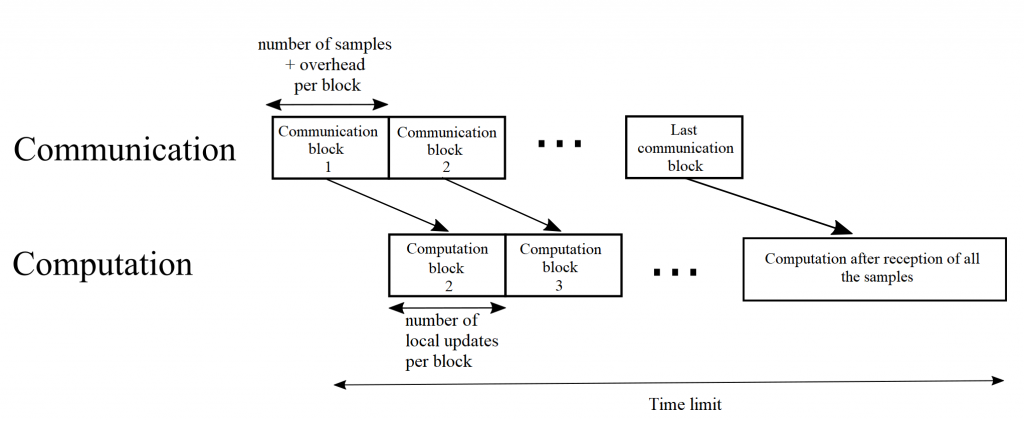
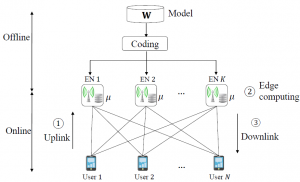 as an enabler of computation-intensive applications on mobile devices. As illustrated in the figure with mobile edge computing, users offload local data to edge servers connected to wireless Edge Nodes (ENs). The ENs in turn carry out the necessary computations and return the desired output to the users on the wireless downlink.
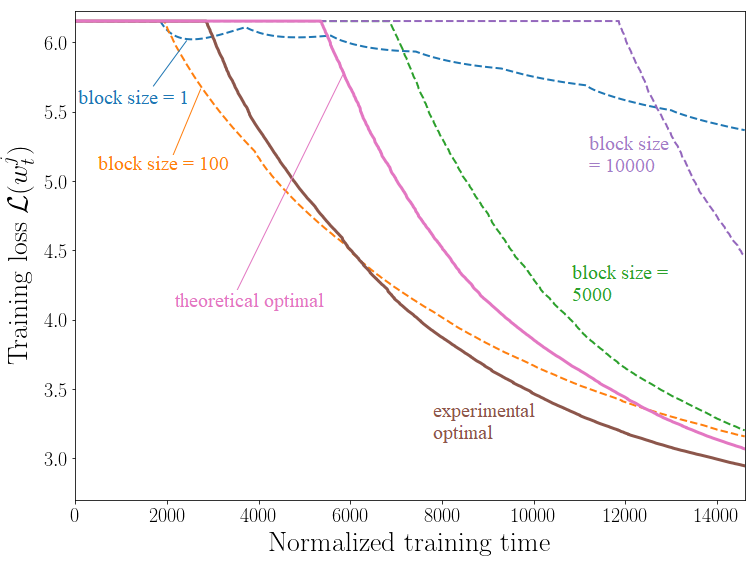
as an enabler of computation-intensive applications on mobile devices. As illustrated in the figure with mobile edge computing, users offload local data to edge servers connected to wireless Edge Nodes (ENs). The ENs in turn carry out the necessary computations and return the desired output to the users on the wireless downlink.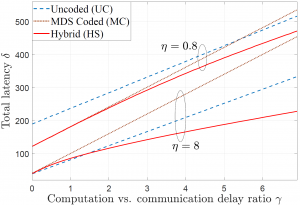 is high, hence this happens for η=0.8, and MDS coding for the most part outperforms the UC scheme due to its robustness to stragglers. This is unless γ is large enough, in which case downlink transmission latency becomes dominant and the UC scheme can benefit from redundant computations via cooperative EN communication. In contrast, when the computing times have low variability, hence for η=8, MDS coding is uniformly outperformed by the UC scheme. The proposed hybrid coding strategy is seen to be effective in trading off computation and communication latencies by controlling the balance between robustness to stragglers and cooperative opportunities.
is high, hence this happens for η=0.8, and MDS coding for the most part outperforms the UC scheme due to its robustness to stragglers. This is unless γ is large enough, in which case downlink transmission latency becomes dominant and the UC scheme can benefit from redundant computations via cooperative EN communication. In contrast, when the computing times have low variability, hence for η=8, MDS coding is uniformly outperformed by the UC scheme. The proposed hybrid coding strategy is seen to be effective in trading off computation and communication latencies by controlling the balance between robustness to stragglers and cooperative opportunities.
Recent Comments