Month: December 2022

Neuromorphic Integrated Sensing and Communications

12/22/2022 / / 0 Comments

Integrated sensing and communications (ISAC), a key enabling technology for 6G systems, leverages shared radio resources and hardware to realize the functions of sensing and communication. As an example of an application that can benefit from ISAC, consider the inter-vehicle communication scenario in Fig. 1. In it, a car wishes to send a message to a second car, while also enabling the latter to detect the presence of a possible target, e.g., of a pedestrian. While conventional systems would use two separate radio resources for data transmission and radar detection, ISAC solutions reuse the same transmitted waveform for the dual role of carrier of digital information and radar signal [1]. A natural radio interface to serve this dual function is impulse radio (IR), also known as ultrawideband (UWB). In fact, IR encodes information in the timing of pulses, which can in turn be repurposed for radar detection [2].

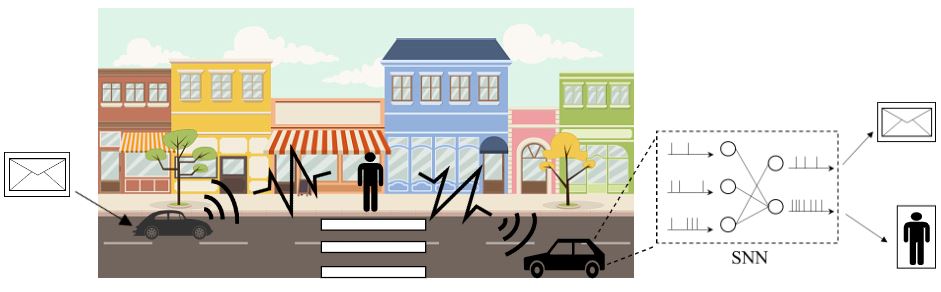
Fig. 1. Illustration of a neuromorphic ISAC system, in which the same IR (or UWB) signal is used for transmission and radar detection of the presence of a target. The key novel element is the use of neuromorphic computing at the ISAC receiver to simultaneously demodulate digital data and provide an online estimate of the presence or absence of the radar target.

Neuromorphic sensing and computing are emerging as alternative, brain-inspired, paradigms for efficient data collection and semantic signal processing [3]. The main features of this technology are energy efficiency, native event-driven processing of time-varying semantic sources, spike-based computing, and always-on on-hardware adaptation [4]. Neuromorphic processors, also known as spiking neural networks (SNNs), are networks of dynamic spiking neurons that mimic the operation of biological neurons. When implemented on specialized — digital or mixed analog-digital — hardware or on tailored FPGA configurations, SNNs have minimal idle and operating energy cost, and consume as little as a few picojoules per spike [5].

The integration of IR and neuromorphic computing was investigated in our recent works [6, 7], which proposed an end-to-end neuromorphic architecture for remote inference that replaces traditional digital blocks with SNNs as encoder and decoder.

Our work

With the aim of reducing energy consumption and facilitating online and always-on operation on specialized hardware, as illustrated in Fig. 1, we propose to leverage the synergy between IR transmission and neuromorphic computing to realize efficient ISAC systems. The neuromorphic ISAC (N-ISAC) receiver is able to leverage spiking neural network (SNN)-based processing to demodulate digital information and detect the radar signal.

As illustrated in Fig. 2, we consider an ISAC system in which digital communication and radar sensing leverage the same IR transmitted signal. In order to efficiently and simultaneously decode the digital data and detect the possible presence of a target at a known delay cell, the receiver processes the received signal via an SNN. Technical details can be found in our paper at this link.

Fig. 2. N-ISAC: Digital data is transmitted by an IR transmitter via pulse-position modulation (PPM); while the receiver simultaneously decodes digital data, and performs radar detection by means of an SNN, which can be efficiently implemented on neuromorphic hardware.

Result

We compare the proposed N-ISAC system with a conventional separate sensing and communications (SSAC) scheme, which divides the transmission slots into slots used for transmission and slots used for sensing. For SSAC, two SNNs are implemented at the receiver, one performing data decoding for the transmission slots, and the other responsible for radar sensing in the sensing slots.

To evaluate the performance of our system, we adopt the following performance metrics for data transmission and radar sensing: 1) Normalized test throughput, i.e., the ratio of the average number of correctly decoded bits over the total number of time slots; 2) Radar test detection error, i.e., the probability that the sensing decision is not correctly taken upon processing all time slots.

In Fig. 3, we demonstrate the normalized test throughput versus the radar test detection error for ISAC and SSAC. For the ISAC scheme, we vary a hyperparameter β dictating the relative weight in the design criterion in favor of communications; for SSAC we vary the fraction α of slots allocated to communications. As β increases, more priority is given by ISAC to communication over radar detection; and, similarly, as α increases, SSAC assigns more slots to communications. The performance of ISAC with an SNN having 10 hidden neurons is essentially independent of β for any 0.25< β <0.75. A first observation is that, for SSAC, there is a trade-off between communication and sensing performance levels caused by the slot allocation. A similar trade-off is also observed for ISAC when using an SNN with 6 hidden neurons. This is due to the limited capacity of the shared common hidden layer of the SNN. In contrast, when 10 hidden neurons are available at the SNN, ISAC is seen to optimize both data decoding and target sensing performance, obtaining significant gains over SSAC.

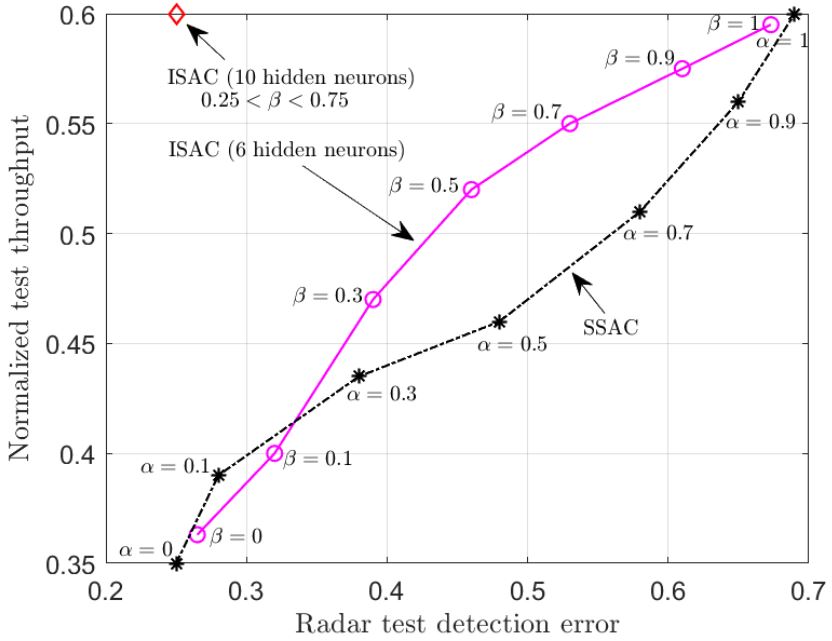
Fig. 3. Normalized test throughput versus radar test detection error for ISAC and SSAC.

Fig. 4 illustrates how the SNN receiver can leverage the temporal sparsity of the IR signals to enhance energy efficiency. In this regard, we recall that energy consumption in an SNN is essentially proportional to the number of spikes produced by the SNN, given extremely low idle energy of neuromorphic chips [8]. The top panel shows the transmitted IR signal consisting of two frames of transmitted signals, separated by an idle frame of duration of 20 slots. We observe that in the idle frame, the spike count is significantly reduced, showing that the neuromorphic receiver can adjust its energy consumption to the activity level of the transmitter.

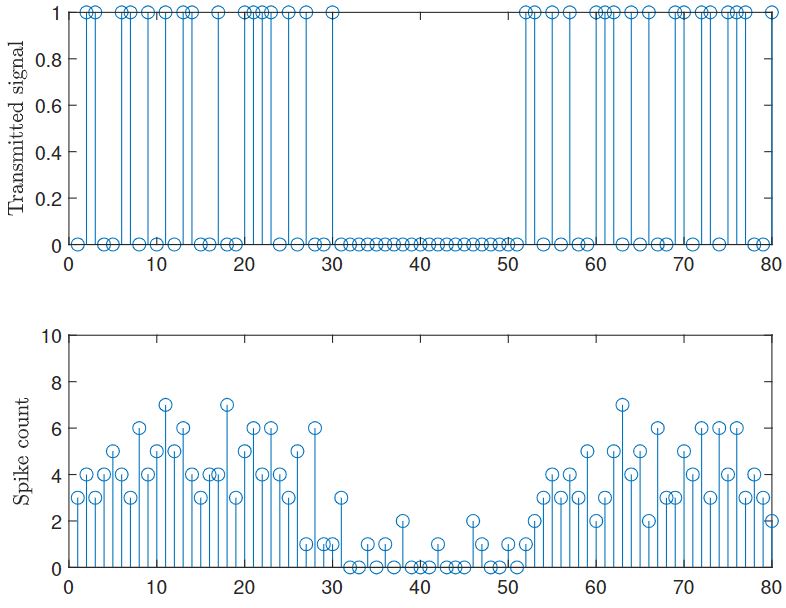
Fig. 4. Top: Transmitted signal consisting of two frames in which the transmitter is active separated by an idle frame. Bottom: Corresponding spike count for the SNN.

References

[1] S. Jeong, O. Simeone, A. Haimovich, and J. Kang, “Beamforming design for joint localization and data transmission in distributed antenna system,” IEEE Transactions on Vehicular Technology, vol. 64, no. 1, pp. 62–76, 2014.

[2] A. Nezirovic, A. G. Yarovoy, and L. P. Ligthart, “Signal processing for improved detection of trapped victims using UWB radar,” IEEE Transactions on Geoscience and Remote Sensing, vol. 48, no. 4, pp. 2005–2014, 2009.

[3] A. Mehonic and A. J. Kenyon, “Brain-inspired computing needs a master plan,” Nature, vol. 604, no. 7905, pp. 255–260, 2022.

[4] M . Davies, A. Wild, G. Orchard, Y. Sandamirskaya, G. A. F. Guerra, P. Joshi, P. Plank, and S. R. Risbud, “Advancing neuromorphic computing with Loihi: a survey of results and outlook,” Proceedings of the IEEE, vol. 109, no. 5, pp. 911–934, 2021.

[5] B. Rajendran, A. Sebastian, M. Schmuker, N. Srinivasa, and E. Eleftheriou, “Low-power neuromorphic hardware for signal processing applications: a review of architectural and system-level design approaches,” IEEE Signal Processing Magazine, vol. 36, no. 6, pp. 97–110, 2019.

[6] N. Skatchkovsky, H. Jang, and O. Simeone, “End-to-end learning of neuromorphic wireless systems for low-power edge artificial intelligence,” in Proc. Asilomar Conference on Signals, Systems, and Computers, pp. 166–173, 2020.

[7] J. Chen, N. Skatchkovsky, and O. Simeone, “Neuromorphic wireless cognition: event-driven semantic communications for remote inference,” arXiv preprint arXiv:2206.06047, 2022.

[8] M . Davies, N. Srinivasa, T.-H. Lin, G. Chinya, Y. Cao, S. H. Choday, G. Dimou, P. Joshi, N. Imam, S. Jain et al., “Loihi: A neuromorphic manycore processor with on-chip learning,” IEEE Micro, vol. 38, no. 1, pp. 82–99, 2018.

 

 

Learning to Learn How to Calibrate

12/08/2022 / / 0 Comments

As discussed in our previous post ‘Is Accuracy Sufficient for AI in 6G? (No, Calibration is Equally Important)’, reliable AI should be able to quantify its uncertainty, i.e., to “know when it knows” and “know when it does not know”. To obtain reliable, or well-calibrated, AI models, two types of approaches can be adopted: (i) training-based calibration, and (ii) post-hoc calibration. Training-based calibration modifies the training procedure by accounting for calibration performance, and includes methods such as Bayesian learning [1, 2], robust Bayesian learning [3, 4], and calibration-aware regularization [5]; while post-hoc calibration utilizes validation data to “recalibrate” a probabilistic model, as in temperature scaling [6], Platt scaling [7], and isotonic regression [8]. All these methods have no formal guarantees on calibration, either due to inevitable model misspecification [9], or due to overfitting to the validation set [10, 11]. In contrast, conformal prediction (CP) offers formal calibration guarantees, although calibration is defined in terms of set, rather than probabilistic, prediction [12]. 

Fig. 1. Improvements in calibration can be obtained by either (i) training-based calibration or (ii) post-hoc calibration. Only conformal prediction, a post-hoc calibration approach, provides formal guarantees on calibration via set prediction.

A well-calibrated set predictor is the one that contains the true label with probability no smaller than a predetermined coverage level, say 90%. A set predictor obtained by conformal prediction is provably well calibrated, irrespective of the unknown underlying ground-truth distribution as long as the data examples are exchangeable, or i.i.d. (independent and identically distributed). 

One could trivially build a well-calibrated set predictor by producing the entire label set as the predicted set. However, such set predictor would be completely uninformative, since the size of the set predictor determines how informative the set predictor is. While conformal prediction is always guaranteed to yield reliable set predictors, it may produce large predicted set size in the presence of limited data examples [13]. In our recent work, presented at the NeurIPS 2022 Workshop on Meta-Learning, we have introduced a novel method that enhances the informativeness of CP-based set predictors via meta-learning.

Fig. 2. Meta-learning transfers knowledge from multiple tasks. In our recent paper, we have proposed an application of meta-learning to conformal prediction with the aim of reducing the average prediction set size while preserving formal calibration guarantees.

Meta-learning, or learning to learn, transfers knowledge from multiple tasks to optimize the inductive bias (e.g., the model class) for new, related, tasks [14]. In our recent work, meta-learning was applied to cross-validation-based conformal prediction (XB-CP) [13] to achieve well-calibrated and informative set predictors. As demonstrated in the following figure, the proposed meta-learning approach for XB-CP, termed meta-XB, can reduce the average prediction set size as compared to conventional CP approaches (XB-CP and validation-based conformal prediction (VB-CP) [12]) and to previous work on meta-learning for VB-CP [14], while preserving the formal guarantees on reliability (the predetermined coverage level, 90%, is always satisfied for meta-XB). 

Fig. 3. Average prediction set size (left) and coverage (right) for new tasks as a function of number of meta-training tasks. As compared to conventional CP schemes (VB-CP and XB-CP), meta-learning based approaches (meta-VB and meta-XB) have smaller prediction set size; while the proposed meta-XB guarantees reliability for every task unlike meta-VB that satisfies coverage condition on average over multiple tasks.

For more details including improvements in terms of input-conditional coverage via meta-learning with adaptive nonconformity scores [15], and further experimental results on image classification and communication engineering aspects, please refer to the arXiv posting.

References

[1] O. Simeone, Machine learning for engineers. Cambridge University Press, 2022

[2] J. Knoblauch, et al, “Generalized variational inference: Three arguments for deriving new posteriors,” arXiv:1904.02063, 2019

[3] W. Morningstar, et al “PACm-Bayes: Narrowing the empirical risk gap in the Misspecified Bayesian Regime,” NeurIPS 2021

[4] M. Zecchin, et al, “Robust PACm: Training ensemble models under model misspecification and outliers,” arXiv:2203.01859, 2022

[5] A. Kumar, et al, “Trainable calibration measures for neural networks from kernel mean embeddings,” ICML 2018

[6] C. Guo, et al, “On calibration of modern neural networks,” ICML 2017

[7] J. Platt, et al, “Probabilistic outputs for support vector machines and comparisons to regularized likelihood method,” Advances in Large Margin Classifiers 1999

[8]  B. Zadrozny and C. Elkan “Transforming classifier scores into accurate multiclass probability estimates,” KDD 2022

[9] A. Masegosa, “Learning under model misspecification: Applications to variational and ensemble methods.” NeurIPS 2020

[10] A. Kumar, et al, “Verified Uncertainty Calibration,” NeurIPS 2019

[11] X. Ma and M. B. Blaschko, “Meta-Cal: Well-controlled Post-hoc Calibration by Ranking,” ICML 2021 

[12]  V. Vovk, et al, “Algorithmic Learning in a Random World,” Springer 2005

[13] R. F. Barber, et al, “Predictive inference with the jackknife+,” The Annals of Statistics, 2021

[14] Chen, Lisha, et al. “Learning with limited samples—Meta-learning and applications to communication systems.” arXiv preprint arXiv:2210.02515, 2022.

[14] A. Fisch, et al, “Few-shot conformal prediction with auxiliary tasks,” ICML 2021

[15] Y. Romano, et al, “Classification with valid and adaptive coverage,” NeurIPS 2020

 

© 2024 King's Communications, Learning & Information Processing lab

Theme by Anders Norén — Up ↑