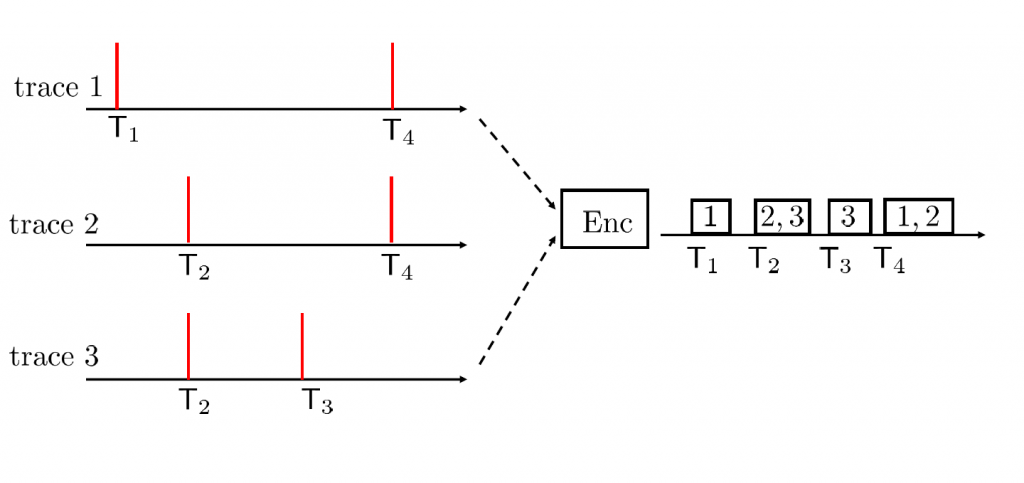
Illustration of the problem of variable length address-event compression with 3 traces: At each events’ occurrence time T_n, the encoder outputs a variable-length packet describing the set of ‘addresses’ of the traces.
Problem Description
The information age has relied on digital information processing: audio, video, and text are represented as strings of bits. Biological brains, however, process information in the timing of events, also known as spikes. Time-encoded information underlies many data types of increasing practical importance, such as social network update times, communication network logs, retweet traces, wireless activity sensors, neuromorphic sensors, and synaptic traces from in-brain measurements for brain-computer interfaces. For example, neuromorphic cameras encode information by producing a spike in response to changes in the sensed environment; and neurons in a Spiking Neural Networks (SNNs) compute and communicate via spiking traces in a way that mimics the operation of biological brains.
When time encoded data is processed at a remote site with respect to the location in which the data is produced, the occurrence of events needs to be encoded and transmitted in a timely fashion. This is particularly relevant in SNN chips for which neurons are partitioned into several cores and spikes produced by neurons in a given core need to be conveyed to the recipient neurons in a separate core in order to enable correct processing. Spikes in SNN’s are encoded into packets through Address Event Representation (AER) protocol. With AER, a packet encoding the occurrence of one or more events is produced at the same time in which the events take place. Thus, the spike timing information is directly carried by the reception of the packet. Therefore, assuming that the packet is detected by the receiver with negligible delay, the packet payload only needs to contain the information about the identity, also referred to as “addresses”, of the “spiking” traces.

A close-up shot of Intel Nahuku board, each of which contains 8 to 32 Intel Loihi neuromorphic chips. (Credit: Tim Herman/Intel Corporation)
In our recent paper accepted for presentation at the IEEE International Symposium on Information Theory and Applications (ISITA 2020), we study the problem of compressing packets generated by an AER-like protocol for generic time-encoded data. This could help alleviate communication bottlenecks in systems that rely on time-encoded data processing.
Suggested Solution
The key idea is that time-encoded traces are characterized by strong correlations both over time and across different traces. These intra-and inter-trace correlations can be harnessed to compress, using variable length codes, the addresses of the event producing traces at a given time.
Towards this, we first model time-encoded data with multiple traces as a discrete-time multi-variate Hawkes process that captures the inter- and intra-trace correlations. This allows formulating the address-event compression problem in terms of the parameters of the discrete-time Hawkes process. Finally, the variable-length compression of packets is achieved through entropy coding via conditional codebooks. The details of the problem modeling can be found here.
Experiment on Real-World Dataset
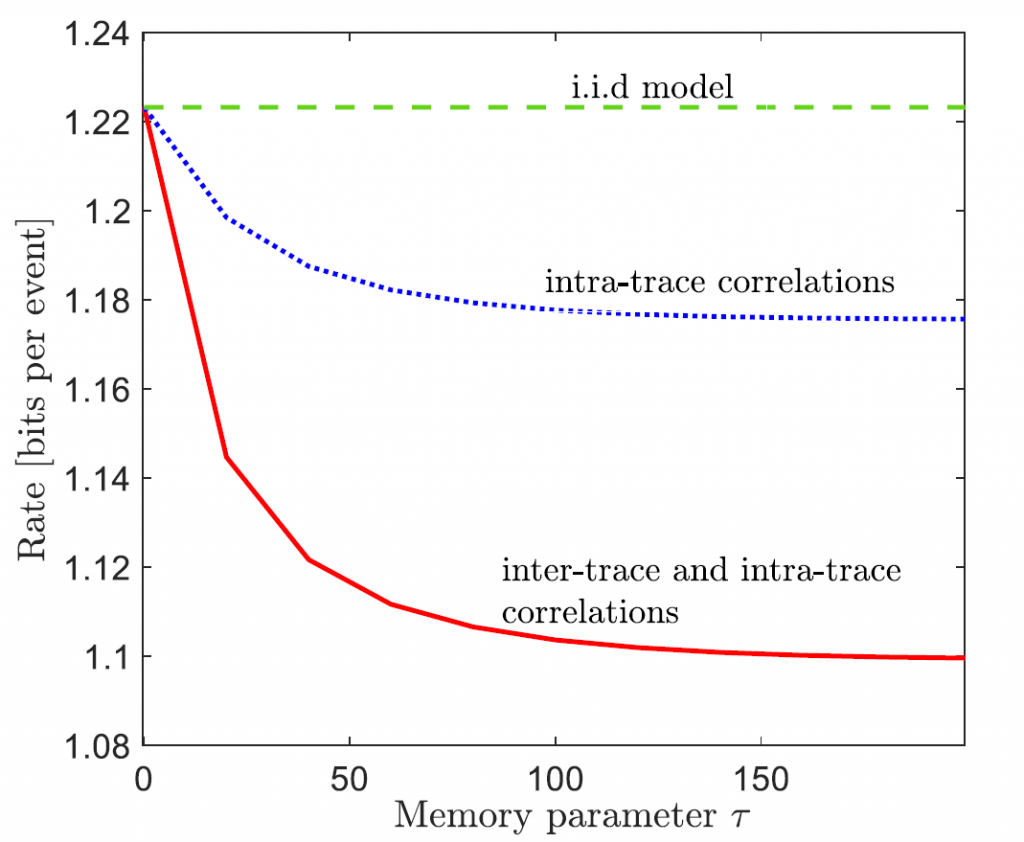
We implemented the proposed variable-length scheme on a real-world retweet dataset. The dataset consists of retweet sequences, each corresponding to the retweets of an original tweet. Each retweet event in a sequence is marked with the type of user group (‘small’, ‘medium’ or, ‘large’) and with the time (quantized to an integer) elapsed since the original tweet. Accordingly, each sequence can be formatted into 3 discrete-time traces. For our experiments, we sampled 2100 sequences from the data set with 2000 sequences used for training and 100 for testing. The training set is used to fit the parameters of the discrete-time Hawkes process. After training, the test sequences are used to evaluate the average number of bits per event, using the trained variable-length code. We study three scenarios: (i) compression with both inter-and intra-trace correlations; (ii) “compression with an i.i.d. model” which assumes the traces to be independent; and (iii) “compression with intra-trace correlation”, which assumes independent traces that are allowed to correlate across time. As seen in the figure below, compared to a no-compression scheme that requires approximately 2.8 bits per event, we find that compression with an i.i.d. model requires only 1.22 bits per event, a gain of 57% over no-compression. Further reductions in rates result from compression schemes that assume intra-trace correlation across time, particularly if accounting also for inter-trace correlations.

Leave a Reply