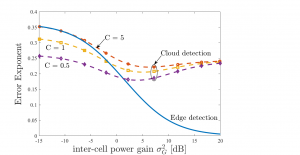
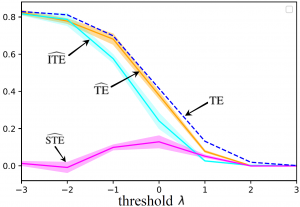
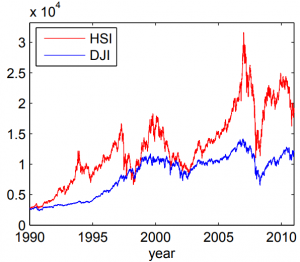
Motivation
When using a machine learning model to make important decisions, like in healthcare, finance, or engineering, we not only need accurate predictions but also want to know how sure the model is about its answers [1-3]. CP offers a practical solution for generating certified “error bars”—certified ranges of uncertainty—by post-processing the outputs of a fixed, pre-trained base predictor. This is crucial for safety and reliability. At the upcoming ISIT 2024 conference, we will present our research work, which aims to bridge the generalization properties of the base predictor with the expected size of the set predictions, also known as informativeness, produced by CP. Understanding the informativeness of CP is particularly relevant as it can usually only be assessed at test time.
Conformal prediction
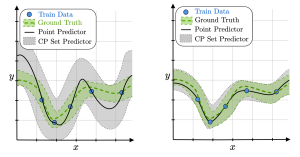
Figure 1: Conformal prediction (CP) set predictors (gray areas) obtained by calibrating a base predictor with a higher generalization error on the left and a lower generalization error on the right. Thanks to CP, both set predictors satisfy a user-defined coverage guarantee, but the inefficiency, i.e., the average prediction set size, is larger when the generalization error of the base predictor is larger.
The most practical form of CP, known as inductive CP, divides the available data into a training set and a calibration set [4]. We use the training data to train a base model, and the calibration data to determine the prediction sets around the decisions made by the base model. As shown in Figure 1, a more accurate base predictor, which generalizes better outside the training set, tends to produce more informative sets when CP is applied.
Results
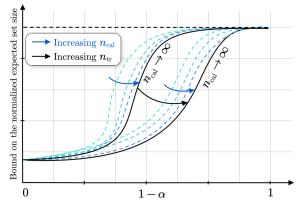
Figure 2: Bound on the average set size for different values of training and calibration data set sizes as a function of the target reliability level. Increasing the number of calibration data points causes the bound to converge exponentially fast to a function (black line) that is increasing in and decreasing in the amount of training data.
Our work’s main contribution is a high probability bound on the expected size of the predicted sets. The bound relates the informativeness of CP to the generalization properties of the base model and the amount of available training and calibration data. As illustrated in Figure 2, our bound predicts that by increasing the amount of calibration data CP’s efficiency converges rapidly to a quantity influenced by the coverage level, the size of the training set, and the predictor’s generalization performance. However, for finite amount of calibration data, the bound is also influenced by the discrepancy between the target and empirical reliability measured over the training data set. Overall, the bound justifies a common practice: allocating more data to train the base model compared to the data used to calibrate it.
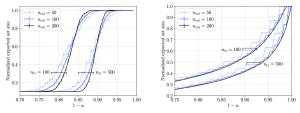
Figure 3: Normalized empirical CP set size for a multi-class classification problem on the MNIST data set as a function of the reliability level and for different sizes of the calibration and training data sets.
Since what really proves the worth of a theory is how well it holds up in real-world testing, we also compare our theoretical findings with numerical evaluations. In our study, we looked at two classification and regression tasks. We ran CP with various splits of calibration and training data, then measured the average efficiency. As shown in the Figure 3, the empirical results from our experiments matched up nicely with what our theory predicted in Figure 2.
References
[1] A. L. Beam and I. S. Kohane, “Big data and machine learning in health care,” JAMA, vol. 319, no. 13, pp. 1317–1318, 2018.
[2] J.. W. Goodell, S. Kumar, W. M. Lim, and D. Pattnaik, “Artificial intelligence and machine learning in finance: Identifying foundations, themes, and research clusters from bibliometric analysis,” Journal of Behavioral and Experimental Finance, vol. 32, p. 100577, 2021.
[3] L. Hewing, K. P. Wabersich, M. Menner, and M. N. Zeilinger, “Learning-based model predictive control: Toward safe learning in control,” Annual Review of Control, Robotics, and Autonomous Systems, vol. 3, pp. 269–296, 2020.
[4] V. Vovk, A. Gammerman, and G. Shafer, Algorithmic learning in a random world, vol. 29. Springer, 2005.

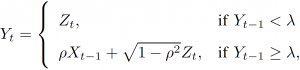
Recent Comments