Month: June 2019

Integrating Wireless Access and Edge Learning

06/19/2019 / / 0 Comments

Problem

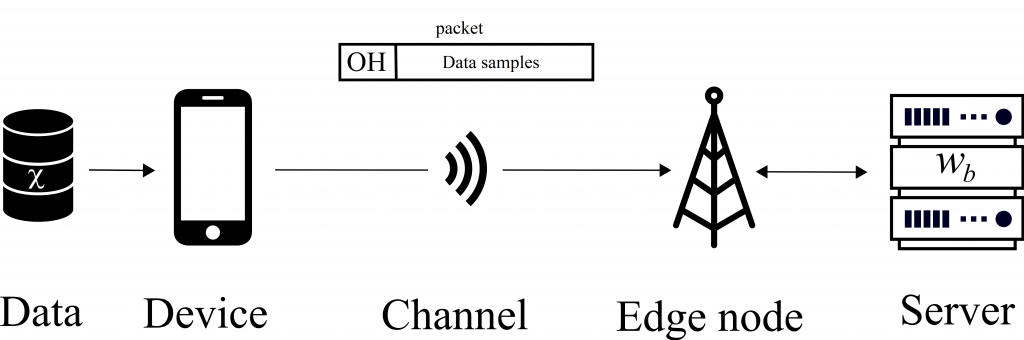
Figure 1. Delay-constrained edge learning based on data received from a device.

The increasing number of connected devices has led to an explosion in the amounts of data being collected: smartphones, wearable devices and sensors generate data to an extent previously unseen. However, these devices often present power and computational capability constraints that do not allow them to make use of the data – for instance, to train Machine Learning (ML) models. In such circumstances, thanks to mobile edge computing, devices can rely on remote servers to perform the data processing (see Fig. 1). When the amount of data is large, or the access link slow, the amount of time required to transmit the data may be prohibitive. Given a delay constraint on the overall time available for both communication and learning, what is the joint communication-computation strategy that obtains the best performing ML model?

Pipelining communication and computation

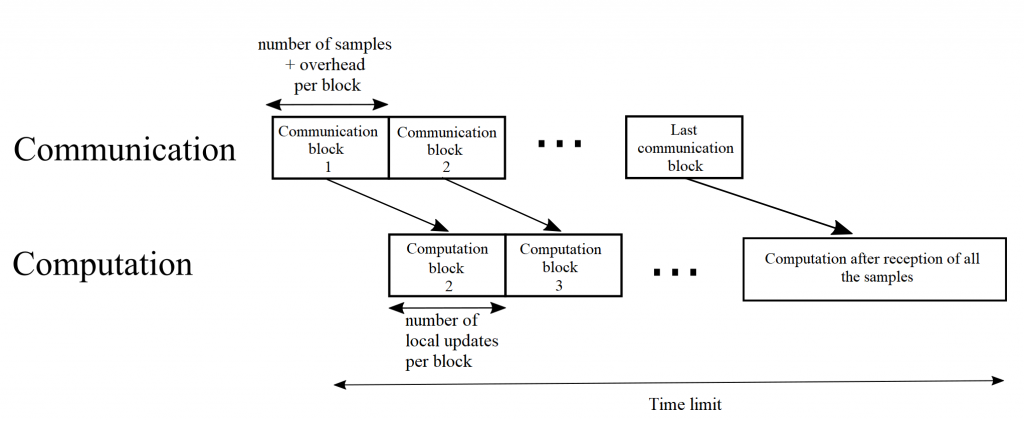
Figure 2. Transmission and training protocol.

In a recent work to be published in IEEE Communication Letters, we propose to pipeline communication and computation with an optimized block size. We consider an Empirical Risk Minimization (ERM) problem, for which learning is carried at the server side using Stochastic Gradient Descent (SGD). As the first data block arrives at the server, training of the ML model can start. This continues by fetching data from all the data blocks received thus far. To provide some intuition on the problem of optimizing the block size, communicating the entire data set first reduces the bias of the training process but it may not leave sufficient time for learning. Conversely, transmitting very few samples in each block will bias the model towards the samples sent in the first blocks, as many computation rounds will happen based on these samples.
We determine an upper bound on the expected optimality gap at the end of the time limit, which gives us an indication on how far we are from an optimal model. We can then minimize this bound with regard to the communication block size to obtain an optimized value.

Some results

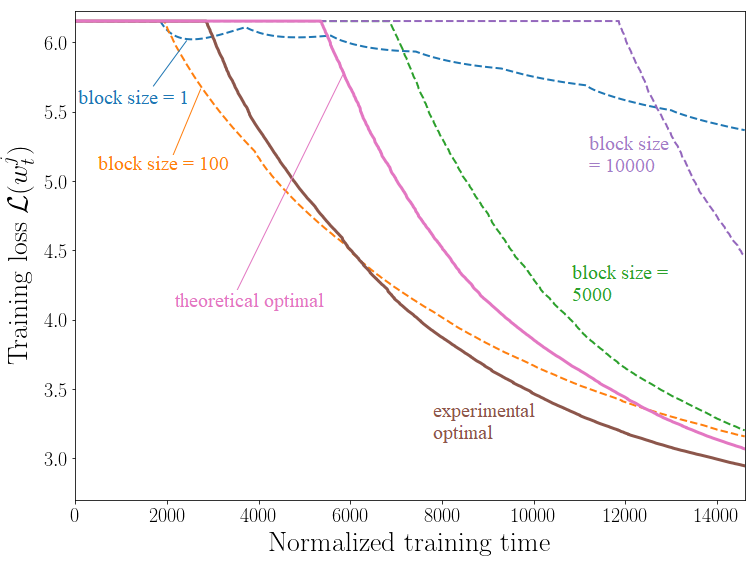
Figure 3. Training loss versus training time for different values of the block size. Solid line: experimental and theoretical optima.

Numerical experiments allowed us to compare the optimal block size found using the bound with a numerically determined optimal value found by running Monte Carlo experiments over all possible block sizes. Determining the optimal value through an extensive search over the possible block sizes allowed a gain of 3.8% in terms of the final training loss in one of our experiments (see Fig. 3). This small gain comes at the cost of a burdensome parameter optimization that took days on an HPC cluster. Minimizing the proposed bound takes seconds.
We further experimentally determined that our results, which were derived for convex loss functions satisfying the Polyak-Lojasiewicz condition, can be extended to non-convex models. As an example (not found in the paper), we studied the problem of training a multilayer perceptron with non-linear activations according to our scheme (see Fig. 4). Using the same dataset as described in the paper, we train a 2-layers perceptron with ReLU activation for the first layer and linear activation for the second. The experiments show a similar behaviour to the convex example discussed in the main text. In particular, the derived bound predicts well the existence of an optimum value of the block size (see crosses).

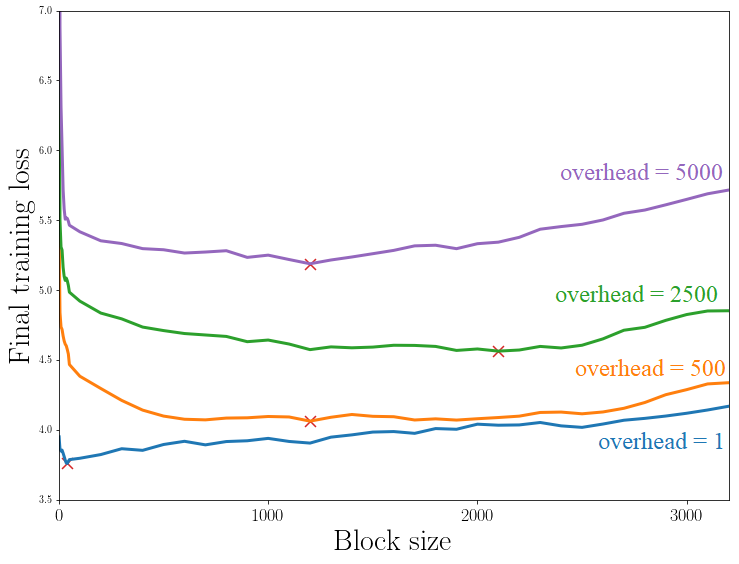
Figure 4. Training loss versus block size for different overhead sizes, for an MLP with non-linear activations.

The full paper can be found here.

Meta-learning: A new framework for few-pilot transmission in IoT networks

06/06/2019 / / 0 Comments

Problem

Fig. 1: Illustration of few-pilot training for an IoT system via meta-learning

For channels with an unknown model or an unavailable optimal receiver of manageable complexity, the design of demodulation and decoding can potentially benefit from a data-driven approach based on machine learning. Machine learning solutions, however, cannot be directly applied to Internet- of-Things (IoT) scenarios in which devices transmit sporadically using short packets with few pilot symbols. In fact, the few pilots do not provide enough data for training the receiver.

A Novel Solution based on Meta-learning

Fig. 2: MAML is to find an initial value 𝜃 that minimizes the loss L𝑘(θ´𝑘) for all devices 𝑘 after one step of update. In contrast, joint training carries out an optimization on the cumulative loss              L1(θ) + L2(θ) 

In a recent work to be presented at IEEE SPAWC 2019, we proposed a novel solution for demodulation in IoT networks that is based on model-agnostic meta-learning (MAML) algorithm. The key idea is to use pilots from previous transmissions of other IoT devices as meta- training data in order to learn a demodulator that is able to quickly adapt to the end-to-end channel conditions of a new device from few pilots. MAML derives an inductive bias as an initialization point for a neural network-based demodulator. As illustrated in Fig. 2, MAML seeks an initialization point such that all the performance losses of the demodulators for all IoT devices obtained after one update are collectively minimized. In comparison, a more conventional approach to use meta-training data, namely joint training, would pool together all the pilots received from the meta-training devices and seeks for minimizing the cumulative loss.

Some Results

To give a taste of the results in the paper, we now provide an example.

Fig. 3: Probability of symbol error with respect to number of pilots for the  meta-test device (see paper).

In Fig. 3, we plot probability of symbol error with respect to the number of pilots for new IoT device in offline scenario. We adopt 16-QAM with 100 meta-training devices, each with 32 pilots for meta-training. We compare the performance of state-of-the-art meta-learning approaches including MAML with: (i) a fixed initialization scheme where data from the meta-training devices is not used; (ii) joint training with the meta-training dataset as described above.

All of the various meta-learning schemes are seen to vastly outperform the mentioned baseline approaches (i) – (ii) by adapting to the channel of the meta-test device using only a few pilots. In contrast, joint training shows similar performance compared to fixed initialization. This confirms that, unlike conventional solutions, meta-learning can effectively transfer information from meta-training devices to a new target device.

 

Fig. 4: Average probability of symbol error with respect to average number of pilots over slots t=71, …, 90 for online meta-learning (see paper).

In Fig. 4, we plot probability of symbol error with respect to average number of pilots in online scenario. Through comparison with fixed initialization case, we have shown that proposed adaptive pilot number selection scheme can reduce pilot overhead with any online schemes. Moreover, when proposed scheme comes with online meta-learning, we show that pilot overhead is reduced even more under negligible performance degradation. This again confirms that meta-learning can acquire useful inductive bias from previous IoT devices.

The full paper can be found here.

© 2024 King's Communications, Learning & Information Processing lab

Theme by Anders Norén — Up ↑