Month: October 2024

Motivation

In machine learning, the information bottleneck (IB) problem [1] is a critical framework used to extract compressed features that retain sufficient information for downstream tasks. However, a major challenge lies in selecting hyperparameters that ensure the learned features comply with information-theoretic constraints. Current methods rely on heuristic tuning without providing guarantees that the chosen features satisfy these constraints. This lack of rigor can lead to suboptimal models. For example, in the context of language model distillation, failing to enforce these constraints may result in the distilled model losing important information from the teacher model.

Our proposed method, “IB via Multiple Hypothesis Testing” (IB-MHT), addresses this issue by introducing a statistically valid solution to the IB problem. We ensure that the features learned by any IB solver meet the IB constraints with high probability, regardless of the dataset size. IB-MHT builds on Pareto testing [2] and learn-then-test (LTT) [3] methods to wrap around existing IB solvers, providing statistical guarantees on the information bottleneck constraints. This approach offers robustness and reliability compared to conventional methods that may not meet these constraints in practice.

IB-MHT

In the traditional IB framework, we aim to minimize the mutual information between the input data X and a compressed representation T, while ensuring that T retains sufficient information about a target variable Y. This is expressed mathematically as minimizing I(X;T) under the constraint that I(T;Y) exceeds a certain threshold. In practice, though, solving this problem often relies on tuning a Lagrange multiplier or hyperparameters to balance the compression of T and the information retained about Y. These approaches do not guarantee that the solution will meet the required information-theoretic constraints.

To overcome this, IB-MHT introduces a probabilistic approach where we wrap around any existing IB solver to ensure that the learned features satisfy the IB constraint with high probability. By leveraging Pareto testing, IB-MHT identifies the optimal hyperparameters through a family-wise error rate (FWER) testing mechanism, ensuring that the final solution is statistically sound.

Experiments

To validate the effectiveness of IB-MHT, we conducted experiments on both classical and deterministic IB [4] formulations. One experiment was performed on the MNIST dataset, where we applied IB-MHT to ensure that the learned representations met the IB constraints with high probability. In another experiment, we applied IB-MHT to the task of distilling language models, transferring knowledge from a large teacher model to smaller student model. We demonstrated that IB-MHT successfully guarantees that the compressed features retain sufficient information about the target variable. Compared to conventional IB methods, IB-MHT showed significant improvements in both the reliability and consistency of the learned representations, with reduced variability in the mutual information estimates.

The following figure illustrates the difference between the performance of conventional IB solvers and IB-MHT in a classical IB setup. While the conventional solver shows a wide variance in the mutual information values, IB-MHT provides tighter control, ensuring that the learned representation T meets the desired information-theoretic constraints.

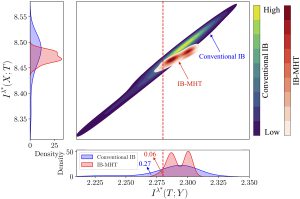
Conclusion

IB-MHT introduces a reliable, statistically valid solution to the IB problem, addressing the limitations of heuristic hyperparameter tuning in existing methods. By guaranteeing that the learned features meet the required information-theoretic constraints with high probability, IB-MHT enhances the robustness and performance of IB solvers across a range of applications. Future work can explore extending IB-MHT to continuous variables and applying similar techniques to other information-theoretic objectives such as convex divergences.

References

[1] Naftali Tishby, Fernando Pereira, and William Bialek. The information bottleneck method. Proceedings of the 37th Allerton Conference on Communication, Control, and Computing, 2001.

[2] Laufer-Goldshtein, Ben, Ariel Fisch, Regina Barzilay, and Tommi Jaakkola. Efficiently controlling multiple risks with Pareto testing. International Conference on Learning Representations, 2023.

[3] Angelopoulos, Anastasios N., Stephen Bates, Emmanuel J. Candès, Michael I. Jordan, and Lucas Lei. Learn then test: Calibrating predictive algorithms to achieve risk control. arXiv preprint arXiv:2110.01052, 2021.

[4] Strouse, Daniel, and David Schwab. The deterministic information bottleneck. Neural Computation, 2017.

Context and Motivations

Neuromorphic processing units (NPUs), such as Intel’s Loihi or BrainChip’s Akida, leverage the sparsity of temporal data to reduce processing energy by activating a small subset of neurons and synapses at each time step. When deployed for split computing in edge-based systems, remote NPUs, each carrying out part of the computation, can reduce the communication power budget by communicating asynchronously using sparse impulse radio (IR) waveforms [1-2], a form of ultra-wide bandwidth (UWB) spread-spectrum signaling.

However, the power savings afforded by sparse transmitted signals are limited to the transmitter’s side, which can transmit impulsive waveforms only at the times of synaptic activations. The main contributor to the overall energy consumption remains the power required to maintain the main radio on.

Architecture

To address this architectural problem, as seen in the figure above, our recent work [3-4] proposes a novel architecture that integrates a wake-up radio mechanism within a split computing system consisting of remote, wirelessly connected, NPUs. In the proposed architecture, the NPU at the transmitter side remains idle until a signal of interest is detected by the signal detection module. Subsequently, a wake-up signal (WUS) is transmitted by the wake-up transmitter over the channel to the wake-up receiver, which activates the main receiver. The IR transmitter modulates the encoded signals from the NPU, and sends them to the main receiver. The NPU at the receiver side then decodes the received signals and make an inference decision.

Digital twin-aided design methodology with reliability guarantee

A key challenge in the design of a wake-up radios is the selection of thresholds for sensing and WUS detection, and decision making (three λ’s in the figure above). A conventional solution would be to calibrate the thresholds via on-air testing, trying out different thresholds via testing on the actual physical system. On-air calibration would be expensive in terms of spectral resources, and there is generally no guarantee that the selected thresholds would provide desirable performance levels for the end application.

To address this design problem, as illustrated in the figure below, this work proposes a novel methodology, dubbed DT-LTT,  that leverages the use of a digital twin, i.e., a simulator, of the physical system, coupled with a sequential statistical testing approach that provides theoretical reliability guarantees. Specifically, the digital twin is leveraged to pre-select a sequence of hyperparameters to be tested using on-air calibration via Learn then Test (LTT) [5]. The proposed DT-LTT calibration procedure is proved to guarantee reliability of the receiver’s decisions irrespective of the fidelity of digital twin and of the data distribution.

Experiment

We compare the proposed DT-LTT calibration method with conventional neuromorphic wireless communications without wake-up radio, conventional LTT without a digital twin, and DT-LTT with an always-on main radio system. As shown in the figure below, the conventional calibration scheme fails to meet the reliability requirement, while the basic LTT scheme selects conservative hyperparameters, often including all classes in the predicted set, which results in zero expected loss. In contrast, the proposed DT-LTT schemes are guaranteed to meet the probabilistic reliability requirement.

References

[1] J. Chen, N. Skatchkovsky and O. Simeone, “Neuromorphic Wireless Cognition: Event-Driven Semantic Communications for Remote Inference,” in IEEE Transactions on Cognitive Communications and Networking, vol. 9, no. 2, pp. 252-265, April 2023,.

[2] J. Chen, N. Skatchkovsky and O. Simeone, “Neuromorphic Integrated Sensing and Communications,” in IEEE Wireless Communications Letters, vol. 12, no. 3, pp. 476-480, March 2023.

[3] J. Chen, S. Park, P. Popovski, H. V. Poor and O. Simeone, “Neuromorphic Split Computing with Wake-Up Radios: Architecture and Design via Digital Twinning,” in IEEE Transactions on Signal Processing, Early Access, 2024.

[4] J. Chen, S. Park, P. Popovski, H. V. Poor and O. Simeone, “Neuromorphic Semantic Communications with Wake-Up Radios,” Proc. IEEE 25th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Lucca, Italy, pp. 91-95, 2024.

[5] Angelopoulos, Anastasios N., et al. “Learn then test: Calibrating predictive algorithms to achieve risk control,” arXiv preprint arXiv:2110.01052, 2021.

Motivation

In many online decision-making settings, ensuring that predictions are well-calibrated is crucial for the safe operation of systems. One way to achieve calibration is through adaptive risk control, which adjusts the uncertainty estimates of a machine learning model based on past feedback [1]. This method guarantees that the calibration error over an arbitrary sequence is controlled and that, in the long run, the model becomes statistically well-calibrated if the data points are independently and identically distributed [2]. However, these schemes only ensure calibration when averaged across the entire input space, raising concerns about fairness and robustness. For instance, consider the figure below, which depicts a tumor segmentation model calibrated to identify potentially cancerous areas. If the model is calibrated using images from different datasets, marginal calibration may be achieved by prioritizing certain subpopulations at the expense of others.

A tumor segmentation model is calibrated using data from two sources to ensure that the marginal false negative rate (FNR) is controlled. However, as shown on the right, the error rate for one source is significantly lower than for the other, leading to unfair performance across subpopulations.

Localized Adaptive Risk Control

To address this issue, our recent work at NeurIPS 2024 proposes a method to localize uncertainty estimates by leveraging the connection between online learning in reproducing kernel Hilbert spaces [3] and online calibration methods. The key idea behind our approach is to use feedback to adjust a model’s confidence levels only in regions of the input space that are near observed data points. This allows for localized calibration, tailoring uncertainty estimates to specific areas of the input space. We demonstrate that, for adversarial sequences, the number of mistakes can be controlled. More importantly, the scheme provides asymptotic guarantees that are localized, meaning they remain valid under a wide range of covariate shifts, for instance those induced by considering certain subpopulation of the data.

Experiments

Comparison between the coverage map obtained using adaptive risk control (on the left) and localized adaptive risk control (on the right). Adaptive risk control is unable to deliver uniform coverage across the deployment areas, leading to large regions where the SNR level is unsatisfactory. In contrast, localized adaptive risk control is capable of guaranteeing a more uniform SNR level, improving the overall system coverage.

To demonstrate the fairness improvements of our algorithm, we conducted a series of experiments using standard machine learning benchmarks as well as wireless communication problems. Specifically, in the wireless domain, we considered the problem of beam selection based on contextual information. Here, a base station must select a subset of communication beam vectors to guarantee a level of signal-to-noise ratio (SNR) across a deployment area. Standard calibration methods like adaptive risk control (on the left) result in substantial SNR variation across the area, creating regions where communication is impossible. In contrast, our localized adaptive risk control scheme (on the right) enables the base station to calibrate the beam selection algorithm to match the local uncertainty, providing more uniform coverage throughout the deployment area.

References

[1] Isaac Gibbs and Emmanuel Candes. Adaptive conformal inference under distribution shift. Advances in Neural Information Processing Systems, 34 (2021).

[2] Anastasios Nikolas Angelopoulos, Rina Barber, Stephen Bates. Online conformal prediction with decaying step sizes. Proceedings of the 41st International Conference on Machine Learning. (2024).

[3] Jyrki Kivinen, Alex Smola and Robert C. Williamson. Online Learning with Kernels. Advances in Neural Information Processing Systems, 14 (2001)