Quantum networking, and with it the quantum Internet, rely on the management and exploitation of entanglement. In fact, entangled qubits enable fundamental quantum communication primitives such as teleportation and superdense coding. Practical sources of entangled qubits, such as single-photon detection, are imperfect, producing mixed states with reduced fidelity as compared to ideal, fully entangled, Bell pairs. In order to enhance the fidelity of entangled qubits available at distributed parties, entanglement distillation protocols leverage local operations and classical communication (LOCC). While existing solutions, such as DEJMPS protocol [1] and LOCCNet [2], assume ideal classical communications, we study the case in which communications between the parties holding imperfectly entangled qubits are noisy. As illustrated in Fig. 1, to address this more challenging scenario, we propose the use of quantum machine learning (QML) [3] via parameterized quantum circuits (PQCs).
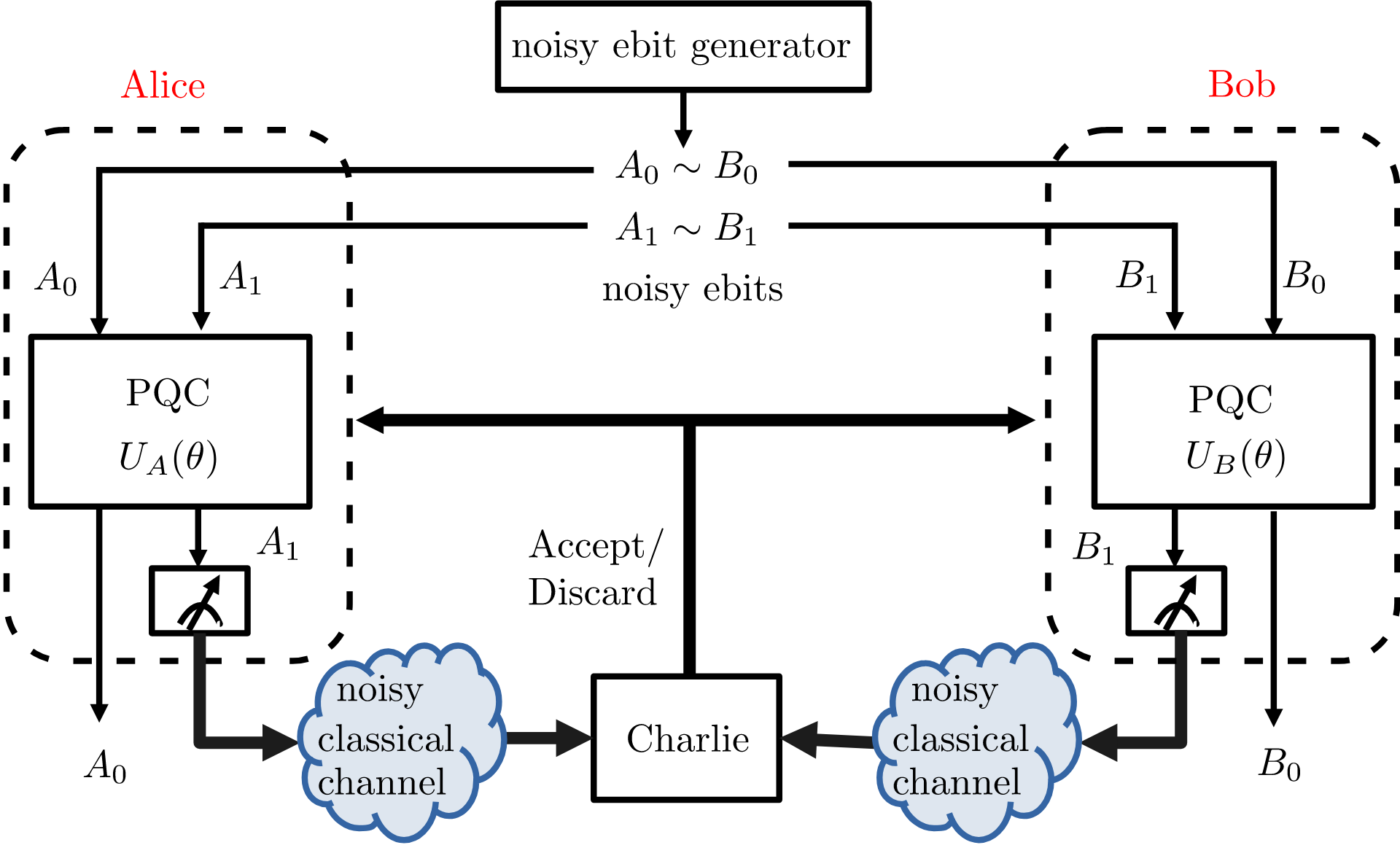
Fig. 1: Entanglement distillation at two quantum-enabled devices (Alice and Bob) aided by a noisy classical communication channel to a third party (Charlie).
Noise Aware-LOCCNet (NA-LOCCNet)
In our recent work, accepted for presentation at IEEE ICASSP 2023, we introduce NA-LOCCNet, as shown in Fig. 2, which improves average output fidelity while accounting for the channel errors.
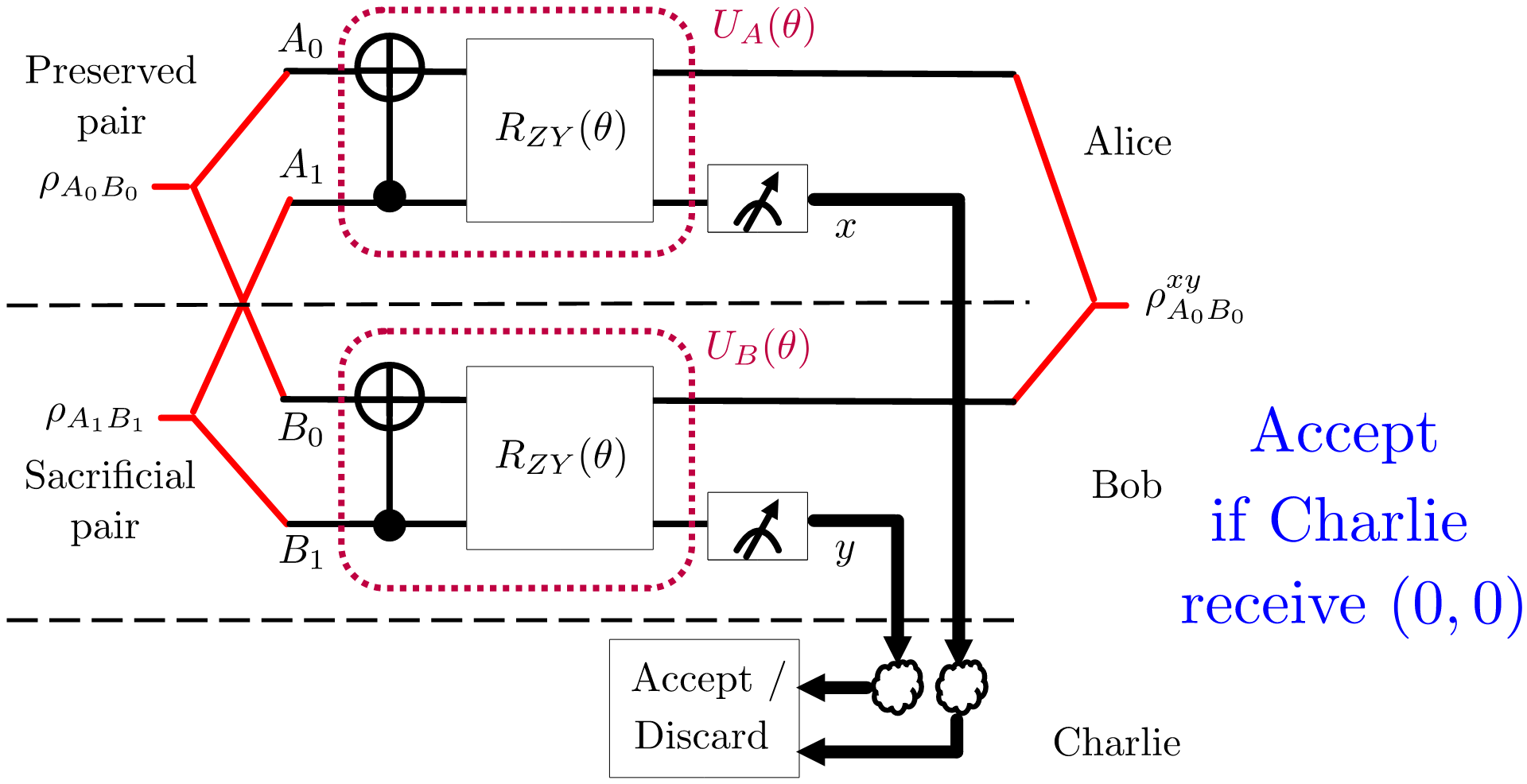
Fig. 2: Proposed Noise Aware-LOCCNet (NA-LOCCNet) circuit for distilling two S states.
Experiments
Fig.3 plots average output fidelity as a function of bit-flip probability of noisy channel for a given input fidelity, whereas Fig. 4 plots the same quantity as a function of input fidelity for a given bit flip probability of noisy channel. In both the figures NA-LOCCNet performs far better than the state of the art protocols.
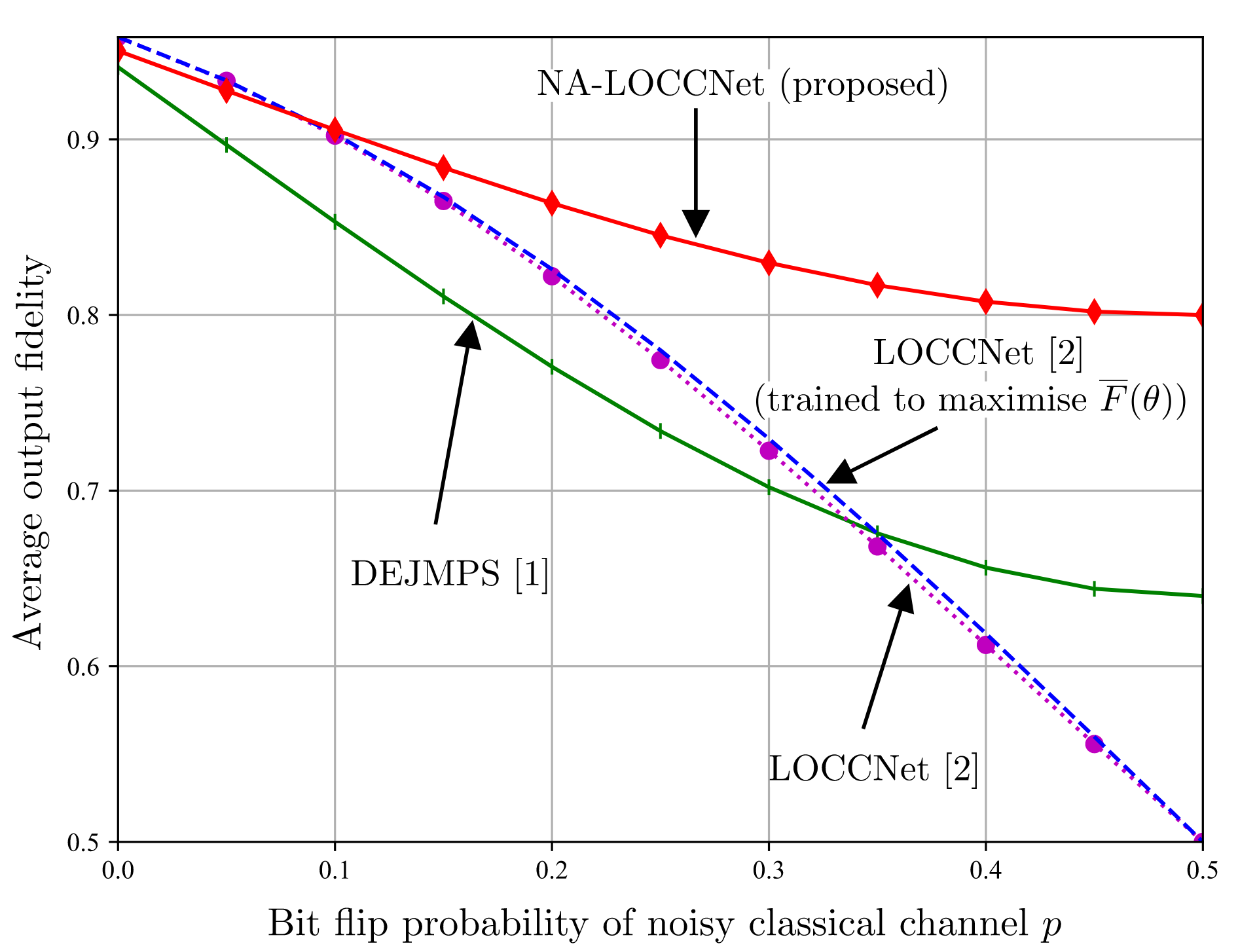
Fig. 3: Average output fidelity as a function of the bit flip probability p of the noisy classical channels from Alice and Bob to Charlie for input fidelity F = 0.6.
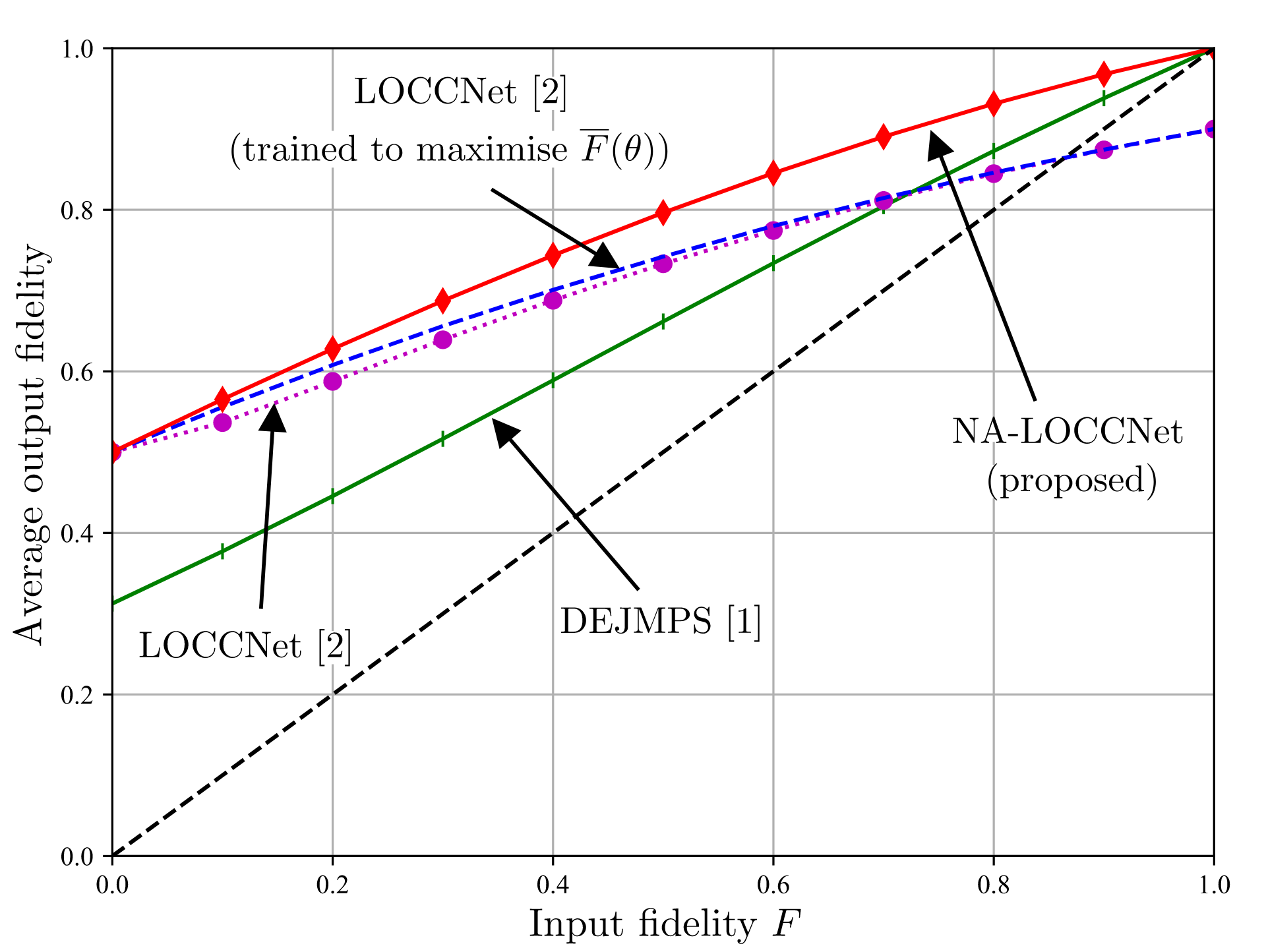
Fig. 4: Average output fidelity, conditioned on a successful distillation, as a function of the input fidelity F for bit flip probability p = 0.25 on the noisy classical channels from Alice and Bob to Charlie. The black dashed line corresponds to the reference performance of a scheme that simply outputs the input state.
In our another recent work, published in Entropy, we have extended the NA-LOCCNet framework to the problem of quantum state discrimination.
[1] D. Deutsch, A. Ekert, R. Jozsa, C. Macchiavello, S. Popescu, and A. Sanpera, “Quantum privacy amplification and the security of quantum cryptography over noisy channels”, Phys. Rev. Lett., vol. 77, pp. 2818– 2821, Sep 1996.
[2] X. Zhao, B. Zhao, Z. Wang, Z. Song, and X. Wang, “Practical distributed quantum information processing with LOCCNet,” Quantum Information, vol. 7, no. 1, pp. 1–7, 2021.
[3] O. Simeone, “An introduction to quantum machine learning for engineers”,
Foundations and Trends in Signal Processing, vol. 16, no. 1-2, pp. 1–223, 2022.

Leave a Reply