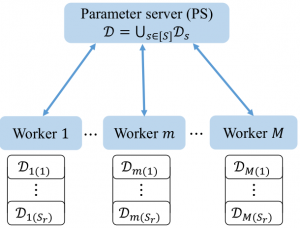
Figure 1: Parameter Server (PS) computing architecture.
Problem Overview:
In order to scale machine learning so as to cope with large volumes of input data, distributed implementations of gradient-based methods, e.g., Gradient Descent (GD), that leverage the parallelism of first-order optimization techniques are commonly adopted. To run GD, as illustrated in Fig.~\ref{fig:model}, multiple parallel workers perform computations of the gradients and the Parameter Server (PS) iteratively aggregates the computed gradients and communicates the updated parameter back to the workers. In the process, the PS computing architecture is subject to two key impairments. First, the potentially high tail of the distribution of the computing times at the workers can cause significant slowdowns in wall-clock run-time per iteration due to straggling workers. Second, the communication overhead resulting from intensive two-way communications between the PS and the workers may require significant networking resources to be available in order not to dominate the overall run-time.
To jointly address these impairments, in a recent work just published on IEEE Transactions on Neural Networks and Learning Systems, we study the performance of coding and lazy aggregation techniques for the PS architecture in terms of wall-clock run-time complexity, communication complexity, and computation complexity.
Main Results:
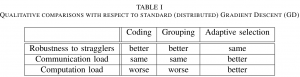
To explore the trade-off among wall-clock time, communication, and computation requirements, we provide a unified analysis of the techniques of gradient coding (GC), worker grouping, and adaptive worker selection, also known as Lazily Aggregated Gradient (LAG), whose relative merits are summarized in Table I. Both GC and grouping are full-gradient approaches that aim at increasing robustness to stragglers by leveraging storage and computation redundancy. Thanks to coding, with GC, only a given number of workers, dependent on the computing redundancy, need to finish their computations and send their encoded computed gradients to the PS at each iteration in order to retrieve the gradient. Grouping applies data duplication and coding to groups of workers. In contrast, LAG is an approximate gradient descent scheme that judiciously selects a subset of active workers at each iteration in order to reduce communication and computation loads. By integrating all the techniques,
we propose a novel strategy, named Lazily Aggregated Gradient Coding (LAGC), that aims at exploring the trade-off between the robustness to stragglers of GC and the computation and communication efficiency of LAG by generalizing both schemes.
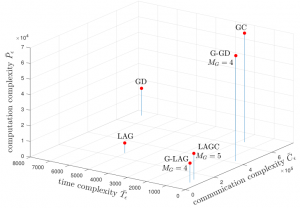
Figure 2: Time, communication, and computation complexity measures under the Pareto distribution.
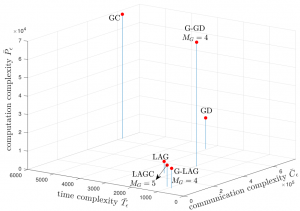
Figure 3: Time, communication, and computation complexity measures under the exponential distribution.
As a special case, we also introduce a scheme that only uses grouping and adaptive selection, which is referred to as G-LAG. For illustration, we consider a linear regression model under two representative distributions, i.e., Pareto distribution and exponential distribution, accounting high- and low-tails for the distribution of the computing times for the workers. Time, communication and computation complexities of the existing strategies, namely GD, GC, and LAG, and the proposed strategies, i.e., LAGC and G-LAG, are shown in Fig. 2 and Fig. 3. It can be seen that both of the proposed LAGC and G-LAG are capable of combining the benefits of gradient coding and grouping in terms of robustness to stragglers with the communication and computation load gains of adaptive selection (see Table I). Furthermore, G-LAG provides the best wall-clock time and communication performance, while maintaining a low computational cost.
The full paper can be found here.

Recent Comments