Author: Amirmohammad Farzaneh

Motivation

Hyperparameter optimization (HPO) is essential in tuning artificial intelligence (AI) models for practical engineering applications, as it governs model performance across varied deployment scenarios. Conventional HPO techniques such as random search and Bayesian optimization often focus on optimizing average performance without providing statistical guarantees, which can be limiting in high-stakes engineering tasks where system reliability is crucial. The learn-then-test (LTT) method [1], introduced in recent research, offers statistical guarantees on the average risk associated with selected hyperparameters. However, in fields like wireless networks and real-time systems, designers frequently need assurance that a specified quantile of performance will meet reliability thresholds.

To address this need, our proposed method, Quantile Learn-Then-Test (QLTT), extends LTT to offer statistical guarantees on quantiles of risk rather than just the average. This quantile-based approach provides greater robustness in real-world applications where it’s critical to control risk-aware objectives, ensuring that the system meets performance goals in a specified fraction of scenarios.

Quantile Learn-Then-Test (QLTT)

LTT, as introduced in [1], guarantees that the average risk remains within a defined threshold with high probability. However, many real-world applications require tighter control over performance measures. For instance, in cellular network scheduling, system designers may need to ensure that key performance indicators (KPIs) like latency and throughput stay within acceptable limits for a majority of users, not just on average.

Our approach, QLTT, extends LTT to provide guarantees on any specified quantile of risk. Specifically, QLTT selects hyperparameters that ensure a predefined quantile of the risk distribution meets a target threshold. This probabilistic guarantee, based on quantile risk control, better aligns with the needs of applications where performance variability is critical.

Methodology

QLTT builds on LTT’s multiple hypothesis testing framework, incorporating a quantile-specific confidence interval, obtained using [2], to achieve guarantees on the desired quantile of risk. The method takes a set of hyperparameter candidates and identifies those that meet the desired quantile threshold with high probability, enhancing reliability beyond what is possible through average risk control alone. This quantile-based approach enables QLTT to adapt to varying risk tolerance levels, making it versatile for different engineering contexts.

Experiments

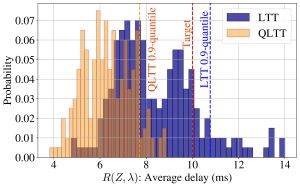
To demonstrate QLTT’s effectiveness, we applied it to a radio access scheduling problem in wireless communication [3]. Here, the task was to allocate limited resources among users with different quality of service (QoS) requirements, ensuring that latency requirements were met for the vast majority of users in real-time.

Our experimental results highlight QLTT’s advantage over LTT with respect to quantile control. While both methods controlled the average risk effectively, only QLTT managed to limit the higher quantiles of the risk distribution, reducing instances where latency exceeded critical thresholds.

The following figure compares the distributions of packet delays for conventional LTT and QLTT for a test run of the simulation. While LTT shows considerable variance, with some instances exceeding the desired threshold, QLTT consistently meets the reliability requirements by providing tighter control over risk quantiles.

Conclusion

QLTT extends the applicability of LTT by providing hyperparameter sets with guarantees on quantiles of a risk measure, thus offering a more rigorous approach to HPO for risk-sensitive engineering applications. Our experiments confirm that QLTT effectively addresses scenarios where quantile risk control is required, providing a robust solution to ensure high-confidence performance across diverse conditions.

Future work may explore expanding QLTT to more complex settings, such as other types of risk functionals and broader engineering challenges. By advancing risk-aware HPO, QLTT represents a significant step toward reliable, application-oriented AI optimization in critical industries.

References

[1] Angelopoulos, A.N., Bates, S., Candès, E.J., Jordan, M.I., & Lei, L. (2021). Learn then test: Calibrating predictive algorithms to achieve risk control. arXiv preprint arXiv:2110.01052.

[2] Howard, S.R., & Ramdas, A. (2022). Sequential estimation of quantiles with applications to A/B testing and best-arm identification. Bernoulli, 28(3), 1704–1728.

[3] De Sant Ana, P.M., & Marchenko, N. (2020). Radio Access Scheduling using CMA-ES for Optimized QoS in Wireless Networks. IEEE Globecom Workshops (GC Wkshps), pp. 1-6.

Motivation

In machine learning, the information bottleneck (IB) problem [1] is a critical framework used to extract compressed features that retain sufficient information for downstream tasks. However, a major challenge lies in selecting hyperparameters that ensure the learned features comply with information-theoretic constraints. Current methods rely on heuristic tuning without providing guarantees that the chosen features satisfy these constraints. This lack of rigor can lead to suboptimal models. For example, in the context of language model distillation, failing to enforce these constraints may result in the distilled model losing important information from the teacher model.

Our proposed method, “IB via Multiple Hypothesis Testing” (IB-MHT), addresses this issue by introducing a statistically valid solution to the IB problem. We ensure that the features learned by any IB solver meet the IB constraints with high probability, regardless of the dataset size. IB-MHT builds on Pareto testing [2] and learn-then-test (LTT) [3] methods to wrap around existing IB solvers, providing statistical guarantees on the information bottleneck constraints. This approach offers robustness and reliability compared to conventional methods that may not meet these constraints in practice.

IB-MHT

In the traditional IB framework, we aim to minimize the mutual information between the input data X and a compressed representation T, while ensuring that T retains sufficient information about a target variable Y. This is expressed mathematically as minimizing I(X;T) under the constraint that I(T;Y) exceeds a certain threshold. In practice, though, solving this problem often relies on tuning a Lagrange multiplier or hyperparameters to balance the compression of T and the information retained about Y. These approaches do not guarantee that the solution will meet the required information-theoretic constraints.

To overcome this, IB-MHT introduces a probabilistic approach where we wrap around any existing IB solver to ensure that the learned features satisfy the IB constraint with high probability. By leveraging Pareto testing, IB-MHT identifies the optimal hyperparameters through a family-wise error rate (FWER) testing mechanism, ensuring that the final solution is statistically sound.

Experiments

To validate the effectiveness of IB-MHT, we conducted experiments on both classical and deterministic IB [4] formulations. One experiment was performed on the MNIST dataset, where we applied IB-MHT to ensure that the learned representations met the IB constraints with high probability. In another experiment, we applied IB-MHT to the task of distilling language models, transferring knowledge from a large teacher model to smaller student model. We demonstrated that IB-MHT successfully guarantees that the compressed features retain sufficient information about the target variable. Compared to conventional IB methods, IB-MHT showed significant improvements in both the reliability and consistency of the learned representations, with reduced variability in the mutual information estimates.

The following figure illustrates the difference between the performance of conventional IB solvers and IB-MHT in a classical IB setup. While the conventional solver shows a wide variance in the mutual information values, IB-MHT provides tighter control, ensuring that the learned representation T meets the desired information-theoretic constraints.

Conclusion

IB-MHT introduces a reliable, statistically valid solution to the IB problem, addressing the limitations of heuristic hyperparameter tuning in existing methods. By guaranteeing that the learned features meet the required information-theoretic constraints with high probability, IB-MHT enhances the robustness and performance of IB solvers across a range of applications. Future work can explore extending IB-MHT to continuous variables and applying similar techniques to other information-theoretic objectives such as convex divergences.

References

[1] Naftali Tishby, Fernando Pereira, and William Bialek. The information bottleneck method. Proceedings of the 37th Allerton Conference on Communication, Control, and Computing, 2001.

[2] Laufer-Goldshtein, Ben, Ariel Fisch, Regina Barzilay, and Tommi Jaakkola. Efficiently controlling multiple risks with Pareto testing. International Conference on Learning Representations, 2023.

[3] Angelopoulos, Anastasios N., Stephen Bates, Emmanuel J. Candès, Michael I. Jordan, and Lucas Lei. Learn then test: Calibrating predictive algorithms to achieve risk control. arXiv preprint arXiv:2110.01052, 2021.

[4] Strouse, Daniel, and David Schwab. The deterministic information bottleneck. Neural Computation, 2017.