Motivation
In machine learning, the information bottleneck (IB) problem [1] is a critical framework used to extract compressed features that retain sufficient information for downstream tasks. However, a major challenge lies in selecting hyperparameters that ensure the learned features comply with information-theoretic constraints. Current methods rely on heuristic tuning without providing guarantees that the chosen features satisfy these constraints. This lack of rigor can lead to suboptimal models. For example, in the context of language model distillation, failing to enforce these constraints may result in the distilled model losing important information from the teacher model.
Our proposed method, “IB via Multiple Hypothesis Testing” (IB-MHT), addresses this issue by introducing a statistically valid solution to the IB problem. We ensure that the features learned by any IB solver meet the IB constraints with high probability, regardless of the dataset size. IB-MHT builds on Pareto testing [2] and learn-then-test (LTT) [3] methods to wrap around existing IB solvers, providing statistical guarantees on the information bottleneck constraints. This approach offers robustness and reliability compared to conventional methods that may not meet these constraints in practice.
IB-MHT
In the traditional IB framework, we aim to minimize the mutual information between the input data X and a compressed representation T, while ensuring that T retains sufficient information about a target variable Y. This is expressed mathematically as minimizing I(X;T) under the constraint that I(T;Y) exceeds a certain threshold. In practice, though, solving this problem often relies on tuning a Lagrange multiplier or hyperparameters to balance the compression of T and the information retained about Y. These approaches do not guarantee that the solution will meet the required information-theoretic constraints.
To overcome this, IB-MHT introduces a probabilistic approach where we wrap around any existing IB solver to ensure that the learned features satisfy the IB constraint with high probability. By leveraging Pareto testing, IB-MHT identifies the optimal hyperparameters through a family-wise error rate (FWER) testing mechanism, ensuring that the final solution is statistically sound.
Experiments
To validate the effectiveness of IB-MHT, we conducted experiments on both classical and deterministic IB [4] formulations. One experiment was performed on the MNIST dataset, where we applied IB-MHT to ensure that the learned representations met the IB constraints with high probability. In another experiment, we applied IB-MHT to the task of distilling language models, transferring knowledge from a large teacher model to smaller student model. We demonstrated that IB-MHT successfully guarantees that the compressed features retain sufficient information about the target variable. Compared to conventional IB methods, IB-MHT showed significant improvements in both the reliability and consistency of the learned representations, with reduced variability in the mutual information estimates.
The following figure illustrates the difference between the performance of conventional IB solvers and IB-MHT in a classical IB setup. While the conventional solver shows a wide variance in the mutual information values, IB-MHT provides tighter control, ensuring that the learned representation T meets the desired information-theoretic constraints.
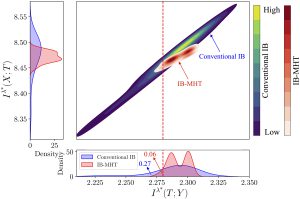
Conclusion
IB-MHT introduces a reliable, statistically valid solution to the IB problem, addressing the limitations of heuristic hyperparameter tuning in existing methods. By guaranteeing that the learned features meet the required information-theoretic constraints with high probability, IB-MHT enhances the robustness and performance of IB solvers across a range of applications. Future work can explore extending IB-MHT to continuous variables and applying similar techniques to other information-theoretic objectives such as convex divergences.
References
[1] Naftali Tishby, Fernando Pereira, and William Bialek. The information bottleneck method. Proceedings of the 37th Allerton Conference on Communication, Control, and Computing, 2001.
[2] Laufer-Goldshtein, Ben, Ariel Fisch, Regina Barzilay, and Tommi Jaakkola. Efficiently controlling multiple risks with Pareto testing. International Conference on Learning Representations, 2023.
[3] Angelopoulos, Anastasios N., Stephen Bates, Emmanuel J. Candès, Michael I. Jordan, and Lucas Lei. Learn then test: Calibrating predictive algorithms to achieve risk control. arXiv preprint arXiv:2110.01052, 2021.
[4] Strouse, Daniel, and David Schwab. The deterministic information bottleneck. Neural Computation, 2017.

Leave a Reply