Context
Quantifying the causal flow of information between different components of a system is an important task for many natural and engineered systems, such as neural, genetic, transportation and social networks. A well-established metric of the information flow between two time sequences ![]() and
and ![]() that has been widely applied for this purpose is the information-theoretic measure of Transfer Entropy (TE). The TE equals the mutual information between the past of sequence
that has been widely applied for this purpose is the information-theoretic measure of Transfer Entropy (TE). The TE equals the mutual information between the past of sequence ![]() and the current value
and the current value ![]() at time t when conditioning on the past of
at time t when conditioning on the past of ![]() . However, the TE has limitations as a measure of intrinsic, or exclusive, information flow from sequence
. However, the TE has limitations as a measure of intrinsic, or exclusive, information flow from sequence ![]() to sequence
to sequence ![]() . In fact, as pointed out in this paper, the TE captures not only the amount of information on
. In fact, as pointed out in this paper, the TE captures not only the amount of information on ![]() that is contained in the past of
that is contained in the past of ![]() in addition to that already present in the past of
in addition to that already present in the past of ![]() , but also the information about
, but also the information about ![]() that is obtained only when combining the past of both
that is obtained only when combining the past of both ![]() and
and ![]() . Only the first type of information flow may be defined as intrinsic, while the second can be thought of as a synergistic flow of information involving both sequences.
. Only the first type of information flow may be defined as intrinsic, while the second can be thought of as a synergistic flow of information involving both sequences.
In the same paper, the authors propose to decompose the TE as the sum of an Intrinsic TE (ITE) and a Synergistic TE (STE), and introduce a measure of the ITE based on cryptography. The idea is to measure the ITE as the size (in bits) of a secret key that can be generated by two parties, one holding the past of sequence ![]() and the other
and the other ![]() , via public communication, when the adversary has the past of sequence
, via public communication, when the adversary has the past of sequence ![]() .
.
The computation of ITE is generally intractable. To estimate ITE, in recent work, we proposed an estimator, referred to as ITE Neural Estimator (ITENE), of the ITE that is based on variational bound on the KL divergence, two-sample neural network classifiers, and the pathwise estimator of Monte Carlo gradients.
Some Results
We first apply the proposed estimator to the following toy example. The joint processes ![]() are generated according to
are generated according to
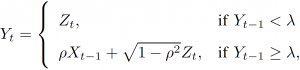
for some threshold λ, where variables ![]() are independent and identically distributed as
are independent and identically distributed as ![]() . Intuitively, for large values of the threshold λ, there is no information flow between
. Intuitively, for large values of the threshold λ, there is no information flow between ![]() and
and ![]() , while for small values, there is a purely intrinsic flow of information. For intermediate values of λ, the information flow is partly synergistic, since knowing both
, while for small values, there is a purely intrinsic flow of information. For intermediate values of λ, the information flow is partly synergistic, since knowing both ![]() and
and ![]() is instrumental in obtaining
is instrumental in obtaining
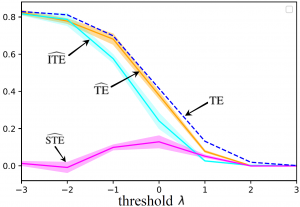
Figure 1
information about ![]() . As illustrated in Fig. 1, the results obtained from the estimator are consistent with this intuition.
. As illustrated in Fig. 1, the results obtained from the estimator are consistent with this intuition.
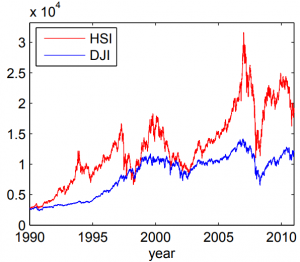
Figure 2
For a real-world example, we apply the estimators at hand to historic data of the values of the Hang Seng Index (HSI) and of the Dow Jones Index (DJIA) between 1990 and 2011 (see Fig. 2). As illustrated in Fig. 3, both the TE and ITE from the DJIA to the HSI are much larger than in the reverse direction, implying that the DJIA influenced the HSI more significantly than the other way around for the
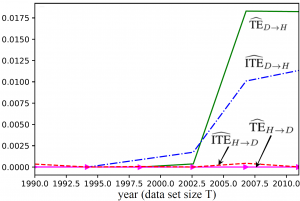
Figure 3
given time range. Furthermore, we observe that not all the information flow is estimated to be intrinsic, and hence the joint observation of the history of the DJIA and of the HSI is partly responsible for the predictability of the HSI from the DJIA.
The full paper will be presented at 2020 International Zurich Seminar on Information and Communication and can be found here.

Recent Comments