Problem

Introduced by the European Telecommunications Standards Institute (ETSI), the concept of mobile edge computing is by now established as a pillar of the 5G network architecture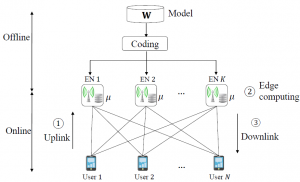 as an enabler of computation-intensive applications on mobile devices. As illustrated in the figure with mobile edge computing, users offload local data to edge servers connected to wireless Edge Nodes (ENs). The ENs in turn carry out the necessary computations and return the desired output to the users on the wireless downlink.

As a baseline application, assume that each user wishes to compute a linear function Wx of a local data vector x, e.g., an image taken by the user’s camera, and a network-side model matrix W. Each EN acquires the users’ local data points x through uplink transmission at runtime, while the matrix W can be pre-stored at the ENs offline. Matrix W is generally large and hence it is split across the servers of multiple ENs. After the computing phase, the ENs transmit the computed outputs back to the users in the downlink.

Linear operations of the type illustrated above are of practical importance. For example, they underlie the implementation of recommendation systems based on collaborative filtering, or similarity searches based on the cosine distance. In both cases, the user-side data is a vector x that embeds the user profile or a query, and the goal is to search through the matrix of all items on the basis of the inner products between the corresponding row of matrix W and the userdata x.

In the presence of storage redundancy, matrix W can be stored at the ENs in uncoded or coded form. In the first case, the rows of the matrix are duplicated across different ENs. As a result, the ENs can transmit any shared computed output back to the users using cooperative transmission techniques. In contrast, with coding, no cooperation transmission is possible but downlink transmission can start as soon as only a subset of ENs has completed computations. The question main is: How should one balance the robustness to straggling ENs afforded by coding with the cooperative downlink transmission advantages of uncoded repetition storage in order to reduce the overall computation-plus-communication latency?

Some Results

Our work investigates three approaches: Uncoded Storage and Computing (UC), MDS coded Storage and Computing (MC), and a proposed Hybrid Scheme (HS) that concatenates an MDS code with a repetition code. The main contribution of this research is to demonstrate that HS is able to combine the robustness to stragglers afforded by MC and the cooperative downlink transmission advantages of UC.

To illustrate this point, consider the figure where we plot overall communication-plus-computation latency as a function of the ratio γ between the communication and computation latencies. The variability in the computing times is defined by a parameter η. It is observed that as γ increases, the total latencies of both UC and MC grow linearly. When the variability in the computing times of the ENs 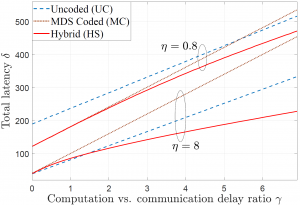is high, hence this happens for η=0.8, and MDS coding for the most part outperforms the UC scheme due to its robustness to stragglers. This is unless γ is large enough, in which case downlink transmission latency becomes dominant and the UC scheme can benefit from redundant computations via cooperative EN communication. In contrast, when the computing times have low variability, hence for η=8, MDS coding is uniformly outperformed by the UC scheme. The proposed hybrid coding strategy is seen to be effective in trading off computation and communication latencies by controlling the balance between robustness to stragglers and cooperative opportunities.

The full paper can be found at ieeexplore (open access: arxiv)