X for Cross Lag

Researchers interested in longitudinal processes can use a range of statistical models to examine how variables are associated over time. One approach often used to examine reciprocal – or bidirectional – associations between variables is the cross-lagged panel model.

---

 

 

 

 

 

What is a cross-lagged panel model?

The cross-lagged panel model (also called longitudinal autoregressive models) is a statistical technique applied to longitudinal data to examine reciprocal or bidirectional associations (i.e., the ‘cross-lagged’ paths) between variables over time. Cross-lagged panel models are tested using structural equation modelling, a broad and flexible statistical tool that allows examining multiple hypotheses simultaneously using different types of variables (for example, binary, ordinal, continuous; Adachi & Willoughby, 2015; Kline, 2023; Selig & Little, 2012). 

By using the cross-lagged panel model, researchers can examine the direction of association between variables and determine whether there are reciprocal influences or bidirectional associations between them. Additionally, this model allows for a more nuanced understanding of how changes in one variable affect changes in another over time, which can be particularly useful when examining complex phenomena such as behaviour change or the development of psychological states.

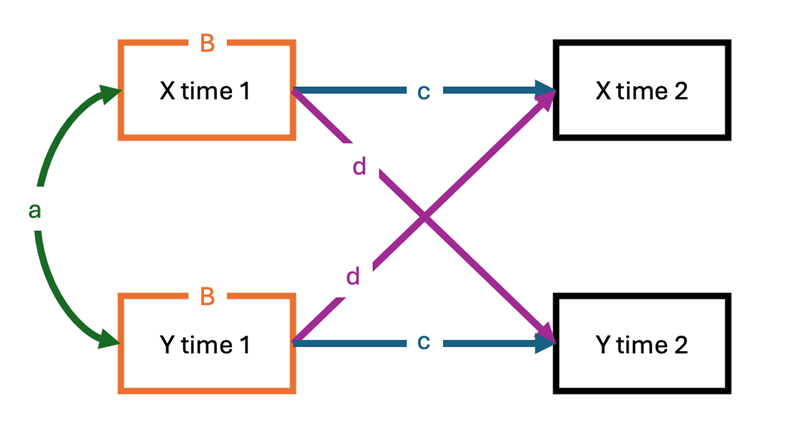
To conduct a cross-lagged panel model, researchers need to collect longitudinal data for at least two variables measured at two different time points. Let’s consider Figure 1 to illustrate the main features of the model. 

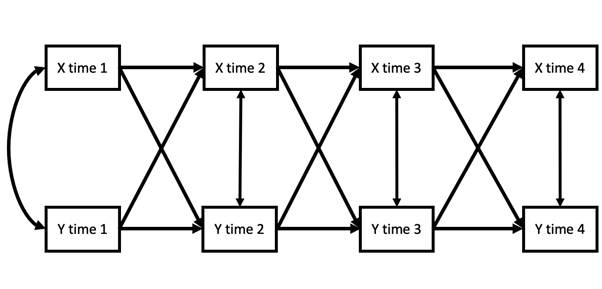
Specifically, the model examines whether one variable is prospectively associated with change in another variable (paths d) by accounting for three elements: 1) baseline levels in both variables (indicated by B), 2) stability over time (paths c), and 3) baseline or previous associations between the variables (correlation a). The model can also be extended to include multiple variables at multiple time points (for example, Figure 2). 

 

Researchers sometimes use the cross-lagged panel model as a way to make causal inference when other methods are not feasible or available. However, it is important to note that while cross-lagged panel models can provide evidence for potential causal relationships, they cannot infer causation without additional assumptions and adjusting for potential confounders (the gold standard for examining causal relationships is randomised control trials). Because researchers typically conduct cross-lagged panel models using longitudinal observational data, it is difficult to rule out all possible alternative sources of explanation for the associations at play such as unmeasured confounders. Therefore, researchers need to consider that other variables not included in the model could still play a role in explaining the findings. As such, it’s important to keep in mind that the model’s utility for making causal inference is limited.

What research questions can be addressed using cross-lagged panel models?

One key feature of the cross-lagged panel model is that it can be used to clarify the directionality of associations. For example, our group recently published a study using a cross-lagged panel model to examine the bidirectional associations between weight and depressive symptoms (Thompson et al., 2023). Results revealed a complex pattern of relationships, where the direction of association between weight and depressive symptoms appeared to be developmentally sensitive. For example, the association was bidirectional between 12 and 16 years old, but thereafter unidirectional, with depressive symptoms at 16 years old predicting weight at 21 years old, but not the reverse. 

These findings underscore the importance of clarifying the direction of associations between weight and depressive symptoms to build effective interventions. In this case for example, the research helps elucidate when a reciprocal relationship between variables is taking place, and what variables are temporarily associated. The results from Thompson et al. (2023) indicated that prevention efforts between ages 12 and 16 years should target both the mechanisms by which weight fluctuations are associated with depression (e.g. weight related stigma), and by which depression is associated with weight fluctuation (e.g. reduction in physical activity).  

Extensions of the cross-lagged panel model

Although the cross-lagged panel model is useful for examining complex longitudinal relationships, it also has some limitations. In 2015, Hamaker and colleagues published a paper in which they highlighted one of the main caveats of the model (Hamaker et al., 2015). They argued that, despite the fact that the cross-lagged panel model accounts for stability within each variable over time, it does not account for other forms of stable factors that could potentially create bias in the associations between variables. These could represent stable trait-like factors like sociodemographic factors or personality traits. 

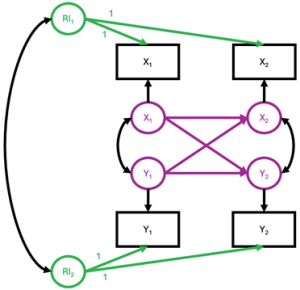
To address this limitation, Hamaker and colleagues (2015) proposed a new model: the random-intercept cross-lagged model. The random-intercept cross-lagged model is somewhat similar to the cross-lagged panel model, but its main additional feature is that it includes latent factors (i.e., the random intercepts; in green in Figure 3). These latent factors account for any potential stable factors that could explain differences between individuals (i.e., between-person differences). By including these latent factors, the model allows for the examination of within-person associations over time or how each individual changes over time (within-person longitudinal associations, in purple in Figure 3), rather than how a group of individuals changes over time (between-person longitudinal associations). It has been argued that by separating between- from within-person effects, the random intercept cross-lagged model is better suited for making inferences about potentially causal relationships (Hamaker et al., 2015). 

Results obtained using cross-lagged panel models often differ from those found using random intercept cross-lagged models. For example, Thompson and colleagues (2023) found bidirectional associations between social isolation and ADHD using a cross-lagged panel model, but found that only ADHD predicted higher subsequent social isolation – and not the reverse – using a random-intercept cross-lagged panel model. These findings suggest that the cross-lagged panel model can produce associations that do not hold in the random-intercept cross-lagged model. As such, the random-intercept cross-lagged model accounts for some of the limitations of the traditional cross-lagged model.

Finally, in addition to the random-intercept cross-lagged model, other extensions of the cross-lagged panel model have been proposed (for example, see Mulder & Hamaker, 2021). Different twin extensions of the model have also been published (e.g., Burt et al., 2005; Malanchini et al., 2017) to examine genetic and environmental influences. Further a recent model has been proposed which includes the use of instrumental variables to measure causation over time in cross-lagged panel models (Singh et al., 2023). These examples illustrate the multiple possibilities and extensions related to the cross-lagged panel model.

In sum, the cross-lagged panel model and its multiple extensions can provide a more comprehensive understanding of the underlying processes at play in complex bidirectional relationships between different outcomes. Nonetheless, as any statistical model, they are not perfect and should always be interpreted in light of their limitations.

 

References

Adachi, P. & Willoughby, T. (2015). Interpreting effect sizes when controlling for stability effects in longitudinal autoregressive models: Implications for psychological science. European Journal of Developmental Psychology, 12(1), 116-128. https://doi.org/10.1080/17405629.2014.963549
Burt, S. A., McGue, M. A. T. T., Krueger, R. F., & Iacono, W. G. (2005). How are parent–child conflict and childhood externalizing symptoms related over time? Results from a genetically informative cross-lagged study. Development and Psychopathology, 17(1), 145-165. https://doi.org/10.1017/S095457940505008X
Hamaker, E. L., Kuiper, R. M., & Grasman, R. P. P. P. (2015). A critique of the cross-lagged panel model. Psychological Methods, 20(1), 102–116. https://doi.org/10.1037/a0038889
Selig, J. P., & Little, T. D. (2012). Autoregressive and cross-lagged panel analysis for longitudinal data. In B. Laursen, T. D. Little, & N. A. Card (Eds.), Handbook of developmental research methods (pp. 265–278). The Guilford Press.
Singh, M., Dolan, C. V., & Neale, M. C. (2023). Integrating cross-lagged panel models with instrumental variables to extend the temporal generalizability of causal inference. Multivariate Behavioral Research, 58(1), 148-149. https://doi.org/10.1080/00273171.2022.2160954
Kline, R. B. (2023). Principles and practice of structural equation modeling (5th ed.). New York, NY: Guilford Press.
Malanchini, M., Wang, Z., Voronin, I., Schenker, V. J., Plomin, R., Petrill, S. A., & Kovas, Y. (2017). Reading self-perceived ability, enjoyment and achievement: A genetically informative study of their reciprocal links over time. Developmental Psychology, 53(4), 698. https://doi.org/10.1037/dev0000209
Mulder, J. D. & Hamaker, E. L. (2020). Three extensions of the random intercept cross-lagged panel model. Structural Equation Modeling: A Multidisciplinary Journal, 28(4), 638-648. https://doi.org/10.1080/10705511.2020.1784738
Thompson, E. J., Krebs, G., Zavos, H., Steves, C., & Eley, T. (2023). The relationship between weight-related indicators and depressive symptoms during adolescence and adulthood: Results from two twin studies. Psychological Medicine, 1-12. https://doi.org/10.1017/S0033291723002155
Thompson, K. N., Agnew-Blais, J. C., Allegrini, A. G., Bryan, B. T., Danese, A., Odgers, C. L., Matthews, T., & Arseneault, L. (2023). Do children with attention-deficit/hyperactivity disorder symptoms become socially isolated? Longitudinal within-person associations in a nationally representative cohort. Journal of the American Academy of Child & Adolescent Psychiatry, 1(1), 12-13. https://doi.org/10.1016/j.jaacap.2023.02.001