One of the great mysteries of introductory programming education is what’s commonly known among computing education practitioners as the double hump.
The double hump refers to the marks distribution in a typical introductory programming course. Here is an example:
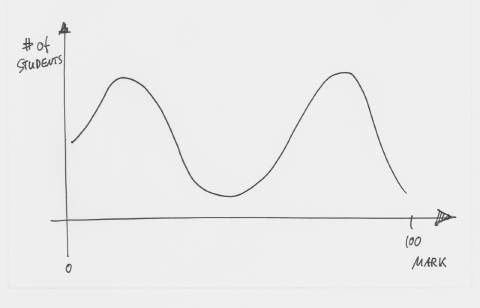
Figure 1: The double hump distribution of marks in a programming course
This graph shows a typical distribution of final marks in a first programming course. We have a whole bunch of students getting very good marks and a lot of them failing. Mark Guzdial, in a blog post, calls it the 20% Rule:
“In every introduction to programming course, 20% of the students just get it effortlessly — you could lock them in a dimly lit closet with a reference manual, and they’d still figure out how to program. 20% of the class never seems to get it.”
The surprising thing about this distribution is how constant it seems to be. It has been observed in programming courses all over the world, largely independent of geographical or social context, and over a long period of time: The same pattern that we observe now existed 10 years ago, and 20 years ago, and 30 years ago.
(And an ironic side note is that we as teachers tend to react to this by aiming our teaching at the medium level—thus teaching to a group that contains hardly any students at all…)
So what is this telling us?
For programming teachers, this poses some interesting questions and challenges. One conclusion has been that the ability to understand programming is somehow intrinsic. That there are people who are just good at it, and others how simply cannot get it. This has led to a whole lot of research about programming ability predictors: ways in which we can predict, by looking at people’s prior activities, performance, social context, or any other aspect of their lives, or with a hopefully simple test, whether or not they will be successful in learning programming before we make them go through it.
Some people really believe in these predictors, some do not. I am generally in the second category. Let’s say, I am at least highly sceptical. The first paper linked above, for example, draws what I believe to be severely invalid conclusions. It interprets the data in a way that the data just does not support. But that’s a story for another day.
What I really want to talk about is an idea that I picked up from a fascinating seminar that Anthony Robins gave a few months ago in our department: That the cause of the high failure rate that we are observing might not be any kind of intrinsic capability, but caused by the sequential nature of the material we are teaching.
What is going on might be this: The material in programming courses is highly hierarchical. Every topic strongly builds on the topics previously covered. Thus, if you don’t understand one section of the course, you will likely also struggle in the following sections, unless you spend extra time to catch up and make up for what you missed before.
Therefore, programming courses are self-amplifying systems. If you fall behind a bit towards the beginning, for whatever reason, you are likely to fall more and more behind in the following weeks and months. If you get ahead early, you are likely to stay ahead, or even move further ahead. The short of it is that this dependancy of performance on prior performance in the course will automatically divide the class into two distinct groups whose performance drifts further apart as time goes on.
Voilá, the double hump is born.
Anthony, in his seminar, made some very interesting points that provided strong indicators that this might be what’s going on. He is, as far as I know, in the process of publishing these findings, so I won’t go into too much detail here. (I will update this post with a link once his paper is out.) We can leave discussion of whether we belive this or not for another day.
For today, I’ll simply state that I find it entirely plausible that this is at the root of the problem. So for now, I will work with the premise that the double hump is not caused by some intrinsic personal capability, but by the strong hierarchical nature of the material we teach.
The question that I asked myself then is: What should we do about it?
My conclusion is that we need to shift from quantity-oriented teaching to quality-oriented teaching. Here is what I mean.
In a typical programming course at a university today, we may have a number of assessments. (For the purpose of this argument it does not matter what that number is—it might be a smaller number of large assessments or a larger number of small ones.) Students get marked on every assessment, and they pass the course if their average grade is above some defined pass level. Figure 2 shows a student in this scheme.
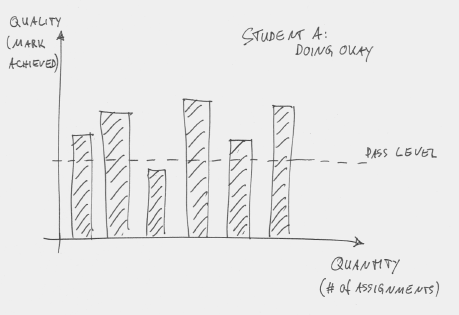
Figure 2: A good student attempts six assessments and passes most of them
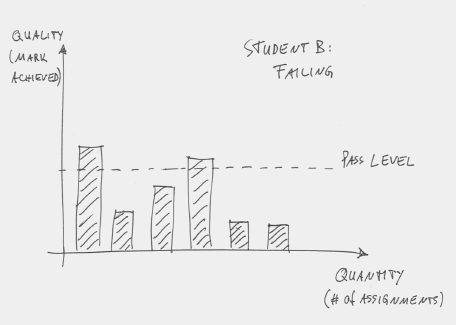
In this example, there are six assessments and the student is doing okay: The average mark is above the pass level. The pattern for a weak student might look like Figure 3: The student also attempts six assessments, but mostly fails.
Figure 3: A weak student attempts six assessments and mostly fails
And this is a problem. It is not only a problem that the student is failing, it is a failure to teach sensibly if we believe in the hierarchical nature of our material. Once the student severely fails Assessment 2, there is really no point to let him/her move on to Assessment 3. In fact, it’s ridiculous. We are essentially saying: “We have just established that you did not understand concept X, so now go on to study concept Y, which is harder and builds on concept X.”
Now, that’s just plainly stupid.
We have essentially demonstrated that you have no chance to move to something harder, and then make you move on to something harder. Without giving you a break to catch up. The problem is: This is exactly what we usually do.
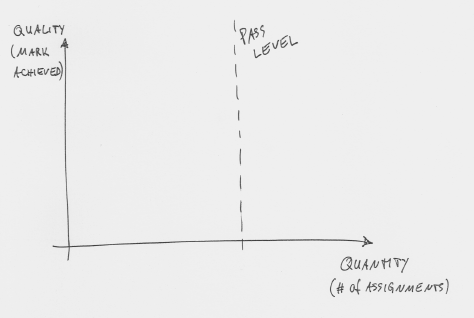
So what can we do about it? The solution might be to re-orient the pass line in our diagram (Figure 4).
Figure 4: Re-thinking the pass level
Typically, in our courses, the x-axis (number of assignment students do) is fixed, while the y-axis (quality of submissions) is variable. And we define success as reaching a given level of quality (see Figure 3).
We should turn that around. We should fix the y-axis and make the x-axis variable, thus re-defining success as successfully completing a certain number of assessments. This means that every student has to achieve a defined minimum level of quality in each assessment before they are allowed to move on to the next assessment. The differentiation between students then is not what quality level they have achieved, but how many stages of assessment they have managed to complete. In a diagram, it looks like this: Figure 5 shows a good student at the end of the course. Nine assessments have been completed, beyond the pass level of assessment 6.
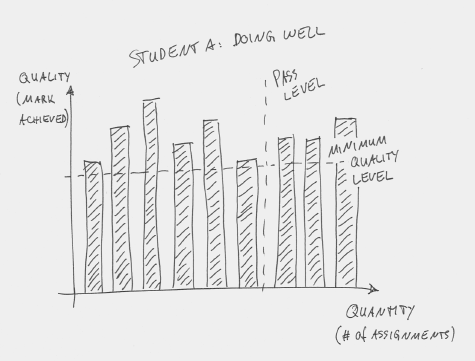
Figure 5: A good student completing enough assessments to pass
The graph for a struggling student then looks like this (Figure 6).
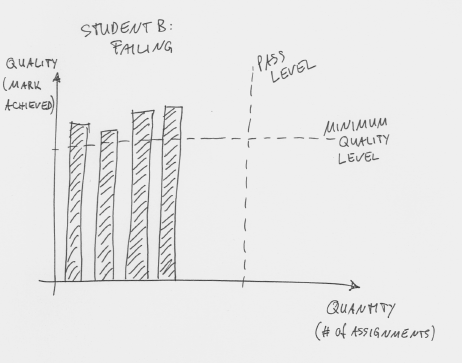
Figure 6: A a struggling students failing to reach pass level
This student has not reached pass level and fails the course. Note, however, the difference here to our student in Figure 3: There are no assessments recorded below the minimum accepted quality level. (Every submission attempt with insufficient quality is simply judged as “not completed”.)
I don’t believe that this scheme will solve all our problems, but I do believe that it has a number of advantages:
- Students may have a higher chance of success. Instead of early failure leading almost automatically to a sequence of further failures, they have a chance to recover.
- Students who learn at different speeds can all survive.
- Especially good students can go even further than they did in the past, because we can allow them to move forward according to their own capabilities.
- More flexibility in dealing with temporary problems: If a student misses the first three weeks of class, be it because of illness or any other reason, they may still pass the class instead of having no chance.
- Even failing students learn something. Instead of failing to understand every topic (Figure 3), they can at least spend their time understanding a few topics (Figure 6).
There are a number of problems and challenges as well, of course. The obvious difficulty is that we must be able to allow different students to work on different material at the same time. Every student effectively progresses at their own personal pace, and the teaching must support this.
Is this organisationally possible? I think so.
It is not easy, and it requires us to severely change how we teach, but I think it’s worth it. It will require different form of instruction (away from big lectures to the whole class) and different form of assessment (away from giving everyone the same task and assessing it by just submitting source code). Otherwise there would be a problem with plagiarism. We might need to assess by interviewing students to actually test their understanding!
Does this create work? Sure. But I think it’s worth it. And I actually believe that, once the change is made, the workload for teachers will be comparable to what we have now.
In an ideal world, this way of learning would have the result that different students learn the same material in a different amount of time. In reality, we will not get away from fixed length courses for the time being.
This means, that—at the end of a course—different students will have studied different amounts of material. Some students who move on to the next course will have covered the advanced material, some have not.
There will be an objection from other teachers that we let students pass who have not seen all the material, and that they do not know some concepts that they should know.
While this is true, I don’t believe that this is any different from our current situation. Which teacher would really claim that all students who passed their course have understood all concepts they were teaching? If one of my current student just barely clears the pass mark, there is a lot that we have covered that they don’t know. Claiming that they know more material because I talked over their heads about more advanced concepts for longer is nonsense.
I would rather have a student who properly understands 50% of the concepts than a student who half understands (and half misunderstands!) everything.


 Computing education in schools is in a dire state—we have known that for some time now.
Computing education in schools is in a dire state—we have known that for some time now.